2024 College Scholastic Ability Test

Mathematics

Multiple Choice Questions
What is the value of \({\sqrt[3]{24} \times 3^{^2/_3}}\)? [2 points]
  1. \(6\)
  2. \(7\)
  3. \(8\)
  4. \(9\)
  5. \(10\)
For the function \(f(x)=2x^3 - 5x^2 + 3\), what is the value of \(\displaystyle\lim_{h\to 0} \dfrac{f(2+h) - f(2)}{h}\)? [2 points]
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)
For \(\theta\) that satisfies \(\dfrac{3}{2}\pi < \theta < 2\pi\) and \(\sin(-\theta) = \dfrac{1}{3}\), what is the value of \(\tan\theta\)? [3 points]
  1. \(-\dfrac{\sqrt{2}}{2}\)
  2. \(-\dfrac{\sqrt{2}}{4}\)
  3. \(-\dfrac{1}{4}\)
  4. \(\dfrac{1}{4}\)
  5. \(\dfrac{\sqrt{2}}{4}\)
If the function
\( f(x) = \begin{cases} 3x-a & \; (x < 2)\\ \\ x^2+a & \; (x \geq 2) \end{cases} \)
is continuous on the set of all real numbers, what is the value of the constant \(a\)? [3 points]
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)

Mathematics

A polynomial function \(f(x)\) satisfies
\(f'(x)=3x(x-2)\:\) and \(\: f(1)=6\).
What is the value of \(f(2)\)? [3 points]
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)
Let \(S_n\) be the sum of the first \(n\) terms of a geometric progression \(\{a_n\}\). Given that
\(S_4 - S_2 = 3a_4\:\) and \(\:a_5=\dfrac{3}{4}\),
what is the value of \(a_1 + a_2\)? [3 points]
  1. \(27\)
  2. \(24\)
  3. \(21\)
  4. \(18\)
  5. \(15\)
The function \(f(x)=\dfrac{1}{3}x^3 - 2x^2 - 12x + 4\) has a local maximum at \(x=\alpha\) and a local minimum at \(x=\beta\). What is the value of \(\beta - \alpha\)?
(※ \(\alpha\) and \(\beta\) are constants.) [3 points]
  1. \(-4\)
  2. \(-1\)
  3. \(2\)
  4. \(5\)
  5. \(8\)

Mathematics

A cubic fuction \(f(x)\) satisfies
\(xf(x) - f(x) = 3x^4 - 3x\)
for all real numbers \(x\).
What is the value of \(\displaystyle\int_{-2}^2 f(x)dx\)? [3 points]
  1. \(12\)
  2. \(16\)
  3. \(20\)
  4. \(24\)
  5. \(28\)
For two points \(\mathrm{P}(\log_5 3)\) and \(\mathrm{Q}(\log_5 12)\) on the number line, if the point internally dividing the line segment \(\mathrm{PQ}\) in the ratio of \(m : (1-m)\) has a coordinate of \(1\), what is the value of \(4^m\)? [4 points]
  1. \(\dfrac{7}{6}\)
  2. \(\dfrac{4}{3}\)
  3. \(\dfrac{3}{2}\)
  4. \(\dfrac{5}{3}\)
  5. \(\dfrac{11}{6}\)
Suppose \(\mathrm{P}\) and \(\mathrm{Q}\) are two points moving on the number line, both starting from the origin at time \(t=0\). The velocity of points \(\mathrm{P}\) and \(\mathrm{Q}\) at time \(t \,(t \geq 0)\) are
\(v_1(t) = t^2-6t+5 \:\) and \(\: v_2(t)=2t-7\)
respectively. Let \(f(t)\) be the distance between points \(\mathrm{P}\) and \(\mathrm{Q}\) at time \(t\). The function \(f(t)\) increases on the interval \([0, a]\), decreases on the interval \([a, b]\), and increases on the interval \([b, \infty)\). What is the distance point \(\mathrm{Q}\) travels from time \(t=a\) to \(t=b\)? [4 points]
  1. \(\dfrac{15}{2}\)
  2. \(\dfrac{17}{2}\)
  3. \(\dfrac{19}{2}\)
  4. \(\dfrac{21}{2}\)
  5. \(\dfrac{23}{2}\)

Mathematics

An arithmetic progression \(\{a_n\}\) whose common difference is not \(0\), satisfies
\(|a_6| = a_8\:\) and \(\displaystyle\:\sum_{k=1}^5 \dfrac{1}{a_k a_{k+1}} = \dfrac{5}{96}\).
What is the value of \(\displaystyle\sum_{k=1}^{15} a_k\)? [4 points]
  1. \(60\)
  2. \(65\)
  3. \(70\)
  4. \(75\)
  5. \(80\)
Let \(f(x) = \dfrac{1}{9} x(x-6)(x-9)\). For a real number \(t \, (0<t<6)\), the function \(g(x)\) is defined as follows.
\( g(x) = \begin{cases} f(x) & \; (x < t)\\ \\ -(x-t)+f(t) & \; (x \geq t) \end{cases} \)
What is the maximum area of the region enclosed by the graph of the function \(y=g(x)\) and the \(x\)-axis? [4 points]
  1. \(\dfrac{125}{4}\)
  2. \(\dfrac{127}{4}\)
  3. \(\dfrac{129}{4}\)
  4. \(\dfrac{131}{4}\)
  5. \(\dfrac{133}{4}\)

Mathematics

As the figure shows, a quadrilateral \(\mathrm{ABCD}\) satisfies
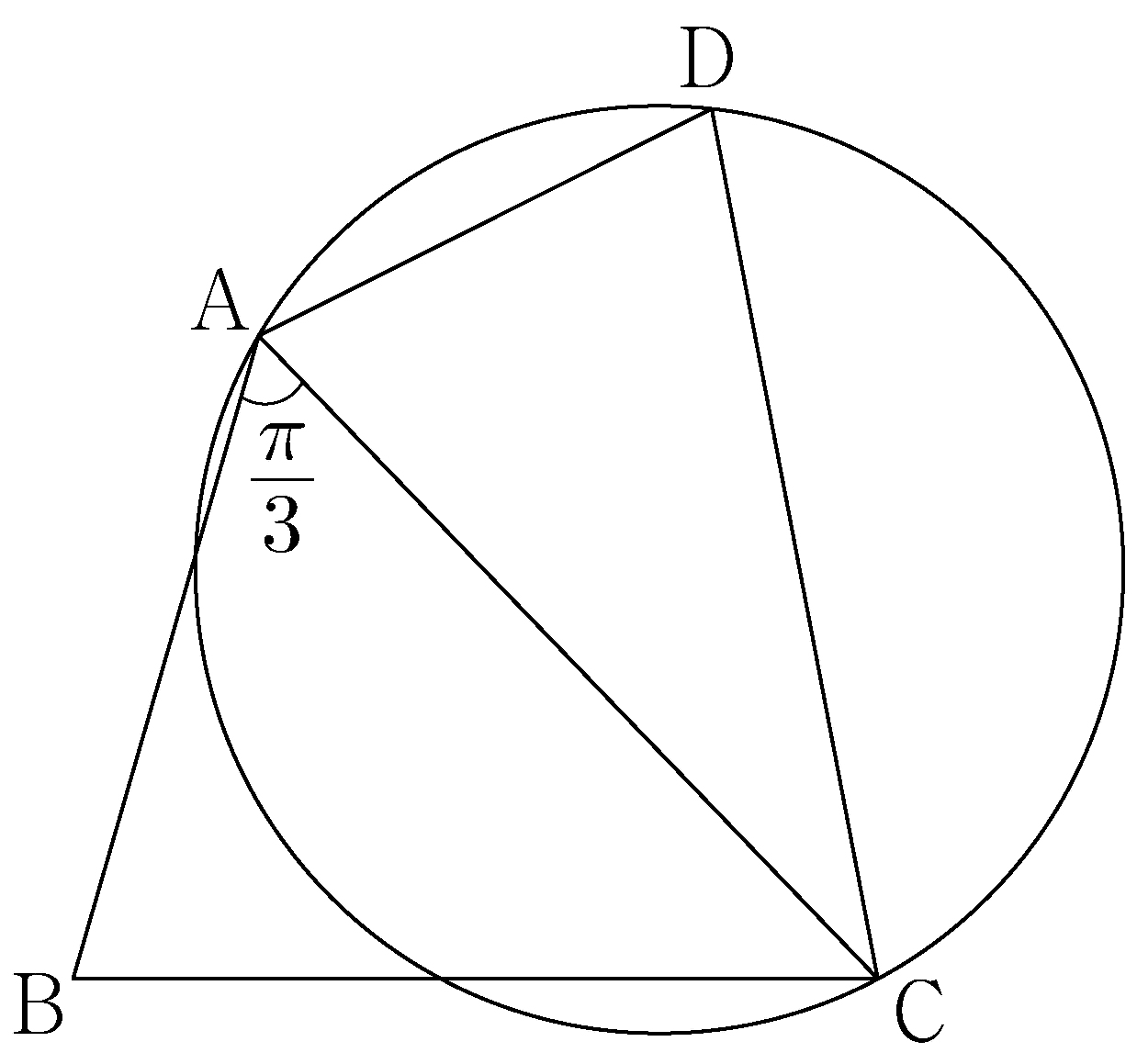
\(\overline{\mathrm{AB}} = 3,\: \overline{\mathrm{BC}} = \sqrt{13},\: \overline{\mathrm{AD}} \times \overline{\mathrm{CD}} = 9\)
and \(\angle \mathrm{BAC} = \dfrac{\pi}{3}\).
Let \(S_1\) be the area of the triangle \(\mathrm{ABC}\), \(S_2\) be the area of the triangle \(\mathrm{ACD}\), and \(R\) be the radius of the circumcircle of the triangle \(\mathrm{ACD}\).
If \(S_2 = \dfrac{5}{6}S_1\), what is the value of \(\dfrac{R}{\sin(\angle \mathrm{ADC})}\)? [4 points]
Figure for question 13
  1. \(\dfrac{54}{25}\)
  2. \(\dfrac{117}{50}\)
  3. \(\dfrac{63}{25}\)
  4. \(\dfrac{27}{10}\)
  5. \(\dfrac{72}{25}\)
A function \(f(x)\) is defined as
\( f(x) = \begin{cases} 2x^3-6x+1 & \; (x \leq 2)\\ \\ a(x-2)(x-b)+9 & \; (x > 2) \end{cases} \)
where \(a\) and \(b\) are positive integers. For a real number \(t\), let \(g(t)\) be the number of points where the graph of the function \(y=f(x)\) meets the line \(y=t\). It is given that there is exactly \(1\) real number \(k\) that satisfies
\(\displaystyle g(k) + \lim_{t\to k-}\!g(t) + \lim_{t\to k+}\!g(t) = 9\).
Among all pairs of positive integers \((a, b)\) that satisfy this condition, what is the maximum value of \(a+b\)? [4 points]
  1. \(51\)
  2. \(52\)
  3. \(53\)
  4. \(54\)
  5. \(55\)

Mathematics

A sequence \(\{a_n\}\) whose initial term is a positive integer, satisfies
\( a_{n+1} = \begin{cases} 2^{a_n} & \; (a_n \text{ is odd})\\ \\ \dfrac{1}{2}a_n & \; (a_n \text{ is even}) \end{cases} \)
for all positive integers \(n\). What is the sum of all values of \(a_1\) for which \(a_6 + a_7 = 3\)? [4 points]
  1. \(139\)
  2. \(146\)
  3. \(153\)
  4. \(160\)
  5. \(167\)
Short Answer Questions
Compute the value of \(x\) that satisfies the equation \(3^{x-8} = \left(\!\dfrac{1}{27}\!\right)^{\!x}\). [3 points]
For the function \(f(x)=(x+1)\!\left(x^2+3\right)\), compute \(f'(1)\). [3 points]

Mathematics

Consider two sequences \(\{a_n\}\) and \(\{b_n\}\), where
\(\displaystyle\sum_{k=1}^{10}a_k = \sum_{k=1}^{10}(2b_k-1)\)
and \(\displaystyle\sum_{k=1}^{10}(3a_k + b_k) = 33\).
Compute \(\displaystyle\sum_{k=1}^{10}b_k\). [3 points]
Let \(f(x)=\sin\dfrac{\pi}{4}x\). For \(0<x<16\), compute the sum of all integers \(x\) for which the inequality
\(f(2+x)f(2-x) < \dfrac{1}{4}\)
is satisfied. [3 points]
A function \(f(x)\) is defined as
\(f(x)=-x^3+ax^2+2x\)
where \(a\) is a real number and \(a>\sqrt{2}\).
Let \(\mathrm{A}\) be the point where a tangent line to the curve \(y=f(x)\) at point \(\mathrm{O}(0, 0)\) meets the curve \(y=f(x)\) again (\(\mathrm{A} \ne \mathrm{O}\)). Let \(\mathrm{B}\) be the point where a tangent line to the curve \(y=f(x)\) at point \(\mathrm{A}\) meets the \(x\)-axis. Given that point \(\mathrm{A}\) is on the circle with the line segment \(\mathrm{OB}\) as a diameter, compute \(\overline{\mathrm{OA}} \times \overline{\mathrm{AB}}\). [4 points]

Mathematics

A function \(f(x)\) is defined on \(x \geq -1\) as
\( f(x) = \begin{cases} -x^2 + 6x & \; (-1 \leq x < 6)\\ \\ a\log_4 (x-5) & \; (x \geq 6) \end{cases} \)
where \(a\) is a positive number. For a real number \(t \geq 0\), let \(g(t)\) be the maximum value of \(f(x)\) over the closed interval \([t-1, t+1]\). Compute the minimum value of the positive number \(a\) for which the minimum value of \(g(t)\) over the interval \([0, \infty)\) is \(5\). [4 points]
A cubic function \(f(x)\) with a leading coefficient of \(1\) satisfies the following.
An integer \(k\) that satisfies
\(f(k-1)f(k+1) < 0\)
does not exist.
Given that \(f'\!\left(\!-\dfrac{1}{4}\!\right) = -\dfrac{1}{4}\:\) and \(\:f'\!\left(\!\dfrac{1}{4}\!\right) < 0\),
compute \(f(8)\). [4 points]

2024 College Scholastic Ability Test

Mathematics (Prob. & Stat.)

Multiple Choice Questions
What is the number of ways to arrange all of the \(5\) letters \(x, x, y, y\) and \(z\) in a straight line? [2 points]
  1. \(10\)
  2. \(20\)
  3. \(30\)
  4. \(40\)
  5. \(50\)
Two events \(A\) and \(B\) are independent. Given that
\(\mathrm{P}(A\cap B) = \dfrac{1}{4}\:\) and \(\:\mathrm{P}\left(A^C\right) = 2\mathrm{P}(A)\),
what is the value of \(\mathrm{P}(B)\)? [3 points]
  1. \(\dfrac{3}{8}\)
  2. \(\dfrac{1}{2}\)
  3. \(\dfrac{5}{8}\)
  4. \(\dfrac{3}{4}\)
  5. \(\dfrac{7}{8}\)

Mathematics (Prob. & Stat.)

There are \(6\) cards marked with numbers \(1, 2, 3, 4, 5\) and \(6\) respectively. If we randomly arrange these \(6\) cards in a line, each card appearing only once, what is the probability that the sum of two numbers written on the cards in each end is no more than \(10\)? [3 points]
  1. \(\dfrac{8}{15}\)
  2. \(\dfrac{19}{30}\)
  3. \(\dfrac{11}{15}\)
  4. \(\dfrac{5}{6}\)
  5. \(\dfrac{14}{15}\)
Figure for question 25 (Prob. & Stat.)
Let us throw \(4\) coins at the same time, and let a random variable \(X\) be the number of coins that land on heads. A discrete random variable \(Y\) is defined as
\( Y= \begin{cases} X & \; (\text{if the value of }X\text{ is }0\text{ or }1)\\ \\ 2 & \; (\text{if the value of }X \geq 2).\\ \end{cases} \)
What is the value of \(\mathrm{E}(Y)\)? [3 points]
  1. \(\dfrac{25}{16}\)
  2. \(\dfrac{13}{8}\)
  3. \(\dfrac{27}{16}\)
  4. \(\dfrac{7}{4}\)
  5. \(\dfrac{29}{16}\)

Mathematics (Prob. & Stat.)

From a population following the normal distribution \(\mathrm{N}\left(m, 5^2\right)\), a sample of size \(49\) was randomly sampled, and the sample mean was \(\overline{x}\). The \(95\%\) confidence interval for the population mean \(m\) computed with this sample is \(a \leq m \leq \dfrac{6}{5}a\). What is the value of \(\overline{x}\)?
(※ For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(|Z| \leq 1.96) = 0.95\).) [3 points]
  1. \(15.2\)
  2. \(15.4\)
  3. \(15.6\)
  4. \(15.8\)
  5. \(16.0\)
There is a sack and two boxes \(\mathrm{A}\) and \(\mathrm{B}\). In the sack there are \(4\) cards marked with numbers \(1, 2, 3\) and \(4\) respectively. In box \(\mathrm{A}\) there are at least \(8\) white balls and black balls each, and box \(\mathrm{B}\) is empty. Let us perform the following trial using the sack and boxes.
Randomly take out a card from the sack, check the number marked on it, and put it back in the sack.
If the checked number is \(1\),
move \(1\) white ball from box \(\mathrm{A}\) to box \(\mathrm{B}\).
If the checked number is \(2\) or \(3\),
move \(1\) white ball and \(1\) black ball from box \(\mathrm{A}\) to box \(\mathrm{B}\).
If the checked number is \(4\),
move \(2\) white balls and \(1\) black ball from box \(\mathrm{A}\) to box \(\mathrm{B}\).
Suppose that after repeating this trial \(4\) times, the number of balls in box \(\mathrm{B}\) is \(8\). What is the probability that the number of black balls in box \(\mathrm{B}\) is \(2\)? [4 points]
  1. \(\dfrac{3}{70}\)
  2. \(\dfrac{2}{35}\)
  3. \(\dfrac{1}{14}\)
  4. \(\dfrac{3}{35}\)
  5. \(\dfrac{1}{10}\)
Figure for question 28 (Prob. & Stat.)

Mathematics (Prob. & Stat.)

Short Answer Questions
Compute the number of \(4\)-tuples \((a, b, c, d)\) where \(a, b, c\) and \(d\) are positive integers less than or equal to \(6\), and satisfies the following. [4 points]
\(a \leq c \leq d\:\) and \(\:b \leq c \leq d\).
A random variable \(X\) follows the normal distribution \(\mathrm{N}\!\left(1, t^2\right)\) where \(t\) is a positive number. Among all positive numbers \(t\) that satisfy
\(\mathrm{P}(X \leq 5t) \geq \dfrac{1}{2}\),
let \(k\) be the maximum value of \(\mathrm{P}\!\left(t^2\!-\!t\!+\!1 \leq\! X \!\leq t^2\!+\!t\!+\!1\right)\), computed using the standard normal table to the right. Compute \(1000\times k\). [4 points]
\(z\)\(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\)
\(0.6\)\(0.226\)
\(0.8\)\(0.288\)
\(1.0\)\(0.341\)
\(1.2\)\(0.385\)
\(1.4\)\(0.419\)

2024 College Scholastic Ability Test

Mathematics (Calculus)

Multiple Choice Questions
What is the value of \(\displaystyle\lim_{x\to 0}\dfrac{\ln(1+3x)}{\ln(1+5x)}\)? [2 points]
  1. \(\dfrac{1}{5}\)
  2. \(\dfrac{2}{5}\)
  3. \(\dfrac{3}{5}\)
  4. \(\dfrac{4}{5}\)
  5. \(1\)
On the curve defined in parametric equations
\(x=\ln\!\left(t^3+1\right)\:\) and \(\:y=\sin\pi t\)
with the parameter \(t\,(t>0)\), what is the value of \(\dfrac{dy}{dx}\) when \(t = 1\)? [3 points]
  1. \(-\dfrac{1}{3}\pi\)
  2. \(-\dfrac{2}{3}\pi\)
  3. \(-\pi\)
  4. \(-\dfrac{4}{3}\pi\)
  5. \(-\dfrac{5}{3}\pi\)

Mathematics (Calculus)

Consider two differentiable functions \(f(x)\) and \(g(x)\) defined on the set of all positive numbers. \(g(x)\) is the inverse of function \(f(x)\), and \(g'(x)\) is continuous on the set of all positive numbers. Given that
\(\displaystyle\int_1^a \!\!\dfrac{1}{g'(f(x))f(x)} dx = 2\ln a + \ln(a+1) - \ln \! 2\)
and \(f(1) = 8\), what is the value of \(f(2)\)? [3 points]
  1. \(36\)
  2. \(40\)
  3. \(44\)
  4. \(48\)
  5. \(52\)
As the figure shows, there is a \(3\)-dimensional solid where one of its faces is the region enclosed by the curve \(y=\sqrt{(1-2x)\cos x}\) \(\left(\!\dfrac{3}{4}\pi \leq x \leq \dfrac{5}{4}\pi\!\right)\),
the \(x\)-axis, and two lines \(x=\dfrac{3}{4}\pi\) and \(x=\dfrac{5}{4}\pi\). Suppose a cross section of this solid and any plane perpendicular to the \(x\)-axis is always a square. What is the volume of this solid? [3 points]
Figure for question 26 (Calculus) (1) Figure for question 26 (Calculus) (2)
  1. \(\sqrt{2}\pi - \sqrt{2}\)
  2. \(\sqrt{2}\pi - 1\)
  3. \(2\sqrt{2}\pi - \sqrt{2}\)
  4. \(2\sqrt{2}\pi - 1\)
  5. \(2\sqrt{2}\pi\)

Mathematics (Calculus)

For a real number \(t\), let \(f(t)\) be the slope of a tangent line to the curve \(y=\dfrac{1}{e^x}+e^t\) that passes through the origin. For a constant \(a\) that satisfies \(f(a) = -e\sqrt{e}\), what is the value of \(f'(a)\)? [3 points]
  1. \(-\dfrac{1}{3}e\sqrt{e}\)
  2. \(-\dfrac{1}{2}e\sqrt{e}\)
  3. \(-\dfrac{2}{3}e\sqrt{e}\)
  4. \(-\dfrac{5}{6}e\sqrt{e}\)
  5. \(-e\sqrt{e}\)
A function \(f(x)\) continuous on the set of all real numbers satisfies \(f(x)\geq 0\) for all real numbers \(x\), and \(f(x) = -4xe^{4x^2}\) for all \(x<0\).
For all positive numbers \(t\), the equation \(f(x)=t\), solved for \(x\), has exactly \(2\) distinct real solutions.
Let \(g(t)\) be the smaller of the solutions and \(h(t)\) be the larger of the solutions.
For all positive numbers \(t\), the functions \(g(t)\) and \(h(t)\) satisfy
\(2g(t)+h(t)=k\:\) (\(k\) is a constant).
If \(\displaystyle\int_0^7 \!\! f(x)dx = e^4-1\), what is the value of \(\dfrac{f(9)}{f(8)}\)? [4 points]
  1. \(\dfrac{3}{2}e^5\)
  2. \(\dfrac{4}{3}e^7\)
  3. \(\dfrac{5}{4}e^9\)
  4. \(\dfrac{6}{5}e^{11}\)
  5. \(\dfrac{7}{6}e^{13}\)

Mathematics (Calculus)

Short Answer Questions
Consider two geometric progressions \(\{a_n\}\) and \(\{b_n\}\) whose initial term and common ratio are not \(0\). It is given that two infinite series \(\displaystyle\sum_{n=1}^\infty a_n\) and \(\displaystyle\sum_{n=1}^\infty b_n\) both converge, and
\(\displaystyle\sum_{n=1}^\infty a_n b_n = \left(\!\sum_{n=1}^\infty a_n\!\!\right) \!\times\! \left(\!\sum_{n=1}^\infty b_n\!\!\right)\)
and \(\:\displaystyle 3\!\times\! \sum_{n=1}^\infty |a_{2n}| = 7\!\times\! \sum_{n=1}^\infty |a_{3n}|\).
Given that \(\displaystyle\sum_{n=1}^\infty \dfrac{b_{2n-1}+b_{3n+1}}{b_n} = S\), compute \(120S\). [4 points]
A function \(f(x)\) is differentiable on the set of all real numbers, and its derivative \(f'(x)\) is
\(f'(x) = |\sin x|\cos x\).
For a positive number \(a\), let \(y=g(x)\) be the equation of the tangent line to the curve \(y=f(x)\) at point \((a, f(a))\). Let us list, in ascending order, all positive numbers \(a\) for which the function
\(\displaystyle h(x)=\int_0^x \!\! \{f(t)-g(t)\}dt\)
has a local maximum or a local minimum at \(x=a\). Let \(a_n\) be the \(n\)th number in this list.
Compute \(\dfrac{100}{\pi} \times (a_6-a_2)\). [4 points]

2024 College Scholastic Ability Test

Mathematics (Geometry)

Multiple Choice Questions
For two points \(\mathrm{A}(a, -2, 6)\) and \(\mathrm{B}(9, 2, b)\) in
\(3\)-dimensional space, if the midpoint of the line segment \(\mathrm{AB}\) has coordinates \((4, 0, 7)\), what is the value of \(a+b\)? [2 points]
  1. \(1\)
  2. \(3\)
  3. \(5\)
  4. \(7\)
  5. \(9\)
What is the slope of the tangent line to the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{6}=1\) at point \((\sqrt{3}, -2)\) on the ellipse?
(※ \(a\) is a positive number.) [3 points]
  1. \(\sqrt{3}\)
  2. \(\dfrac{\sqrt{3}}{2}\)
  3. \(\dfrac{\sqrt{3}}{3}\)
  4. \(\dfrac{\sqrt{3}}{4}\)
  5. \(\dfrac{\sqrt{3}}{5}\)

Mathematics (Geometry)

Two vectors \(\vec{a}\) and \(\vec{b}\) satisfy
\(\big|\vec{a}\big| = \sqrt{11}\), \(\big|\vec{a}\big| = 3\) and \(\big|2\vec{a}-\vec{b}\big| = \sqrt{17}\).
What is the value of \(\big|\vec{a} - \vec{b}\big|\)? [3 points]
  1. \(\dfrac{\sqrt{2}}{2}\)
  2. \(\sqrt{2}\)
  3. \(\dfrac{3\sqrt{2}}{2}\)
  4. \(2\sqrt{2}\)
  5. \(\dfrac{5\sqrt{2}}{2}\)
Consider a plane \(\alpha\) in \(3\)-dimensional space. For two distinct points \(\mathrm{A}\) and \(\mathrm{B}\) both not on plane \(\alpha\), let \(\mathrm{A}'\) and \(\mathrm{B}'\) be their projection onto plane \(\alpha\) respectively. It is given that
\(\overline{\mathrm{AB}} = \overline{\mathrm{A'B'}} = 6\).
Let \(\mathrm{M}\) be the midpoint of the line segment \(\mathrm{AB}\), and \(\mathrm{M}'\) be its projection onto plane \(\alpha\). Let \(\mathrm{P}\) be a point on plane \(\alpha\) such that
\(\overline{\mathrm{PM'}} \perp \overline{\mathrm{A'B'}}\) and \(\overline{\mathrm{PM'}} = 6\).
If the projection of the triangle \(\mathrm{A'B'P}\) onto plane \(\mathrm{ABP}\) has an area of \(\dfrac{9}{2}\), what is the length of the line segment \(\mathrm{PM}\)? [3 points]
  1. \(12\)
  2. \(15\)
  3. \(18\)
  4. \(21\)
  5. \(24\)

Mathematics (Geometry)

A point \(\mathrm{A}\) is on the parabola \(y^2=8x\) with focus \(\mathrm{F}\). Let \(\mathrm{B}\) be the perpendicular foot from point \(\mathrm{A}\) to the directrix of the parabola, and let \(\mathrm{C}\) and \(\mathrm{D}\) be the two intersections of line \(\mathrm{BF}\) and the parabola.
If \(\overline{\mathrm{BC}} = \overline{\mathrm{CD}}\), what is the area of the triangle \(\mathrm{ABD}\)?
(※ \(\overline{\mathrm{CF}} < \overline{\mathrm{DF}}\), and point \(\mathrm{A}\) is not the origin.) [3 points]
  1. \(100\sqrt{2}\)
  2. \(104\sqrt{2}\)
  3. \(108\sqrt{2}\)
  4. \(112\sqrt{2}\)
  5. \(116\sqrt{2}\)
As the figure shows, two points \(\mathrm{A}\) and \(\mathrm{B}\) are on the line of intersection between two distinct planes \(\alpha\) and \(\beta\) where \(\overline{\mathrm{AB}} = 18\). A circle \(C_1\), with the line segment \(\mathrm{AB}\) as a diameter, is on plane \(\alpha\). An ellipse \(C_2\), with the line segment \(\mathrm{AB}\) as the major axis and two points \(\mathrm{F}\) and \(\mathrm{F'}\) as the foci, is on plane \(\beta\).
For a point \(\mathrm{P}\) on circle \(C_1\), let \(\mathrm{H}\) be the perpendicular foot of point \(\mathrm{P}\) to plane \(\beta\). Point \(\mathrm{H}\) satisfies \(\overline{\mathrm{HF'}} < \overline{\mathrm{HF}}\) and \(\angle\mathrm{HFF'}=\dfrac{\pi}{6}\). Among the intersections of line \(\mathrm{HF}\) and the ellipse \(C_2\), let \(\mathrm{Q}\) be the point closest to point \(\mathrm{H}\). Point \(\mathrm{Q}\) satisfies \(\overline{\mathrm{FH}} < \overline{\mathrm{FQ}}\).
A circle on plane \(\beta\), with center \(\mathrm{H}\) and radius \(4\), passes through point \(\mathrm{Q}\) and is tangent to the line \(\mathrm{AB}\). Let \(\theta\) be the angle between two planes \(\alpha\) and \(\beta\). What is the value of \(\cos\theta\)?
(※ Point \(\mathrm{P}\) is not on plane \(\beta\).) [4 points]
Figure for question 28 (Geometry)
  1. \(\dfrac{2\sqrt{66}}{33}\)
  2. \(\dfrac{4\sqrt{69}}{69}\)
  3. \(\dfrac{\sqrt{2}}{3}\)
  4. \(\dfrac{4\sqrt{3}}{15}\)
  5. \(\dfrac{2\sqrt{78}}{39}\)

Mathematics (Geometry)

Short Answer Questions
Consider a hyperbola with foci \(\mathrm{F}(c, 0)\) and \(\mathrm{F'}(-c, 0)\) and a major axis of length \(6\), where \(c\) is a positive number. Compute the sum of all values of \(c\) for which there exist two distinct points \(\mathrm{P}\) and \(\mathrm{Q}\) on the hyperbola that satisfy the following. [4 points]
  1. Point \(\mathrm{P}\) is in the \(1\)st quadrant,
    and point \(\mathrm{Q}\) is on line \(\mathrm{PF'}\).
  2. The triangle \(\mathrm{PFF'}\) is an isosceles triangle.
  3. The perimeter of the triangle \(\mathrm{PQF}\) is \(28\).
There is an equilateral triangle \(\mathrm{ABC}\) with a side length of 4 on the \(xy\)-plane. Let \(\mathrm{D}\) be the point internally dividing the line segment \(\mathrm{AB}\) in the ratio of \(1:3\). Let \(\mathrm{E}\) be the point internally dividing the line segment \(\mathrm{BC}\) in the ratio of \(1:3\). Let \(\mathrm{F}\) be the point internally dividing the line segment \(\mathrm{CA}\) in the ratio of \(1:3\). Four points \(\mathrm{P,Q,R}\) and \(\mathrm{X}\) satisfy the following.
  1. \(|\overrightarrow{\mathrm{DP}}| = |\overrightarrow{\mathrm{EQ}}| = |\overrightarrow{\mathrm{FR}}| = 1\)
  2. \(\overrightarrow{\mathrm{AX}} = \overrightarrow{\mathrm{PB}} + \overrightarrow{\mathrm{QC}} + \overrightarrow{\mathrm{RA}}\)
Let \(S\) be the area of the triangle \(\mathrm{PQR}\) When the value of \(|\overrightarrow{\mathrm{AX}}|\) is the greatest. Compute \(16S^2\). [4 points]