2023 College Scholastic Ability Test

Mathematics

Multiple Choice Questions

What is the value of \({\left(\!\dfrac{4}{2^\sqrt{2}}\!\right)^{\!2+\sqrt{2}}}\)? [2 points]

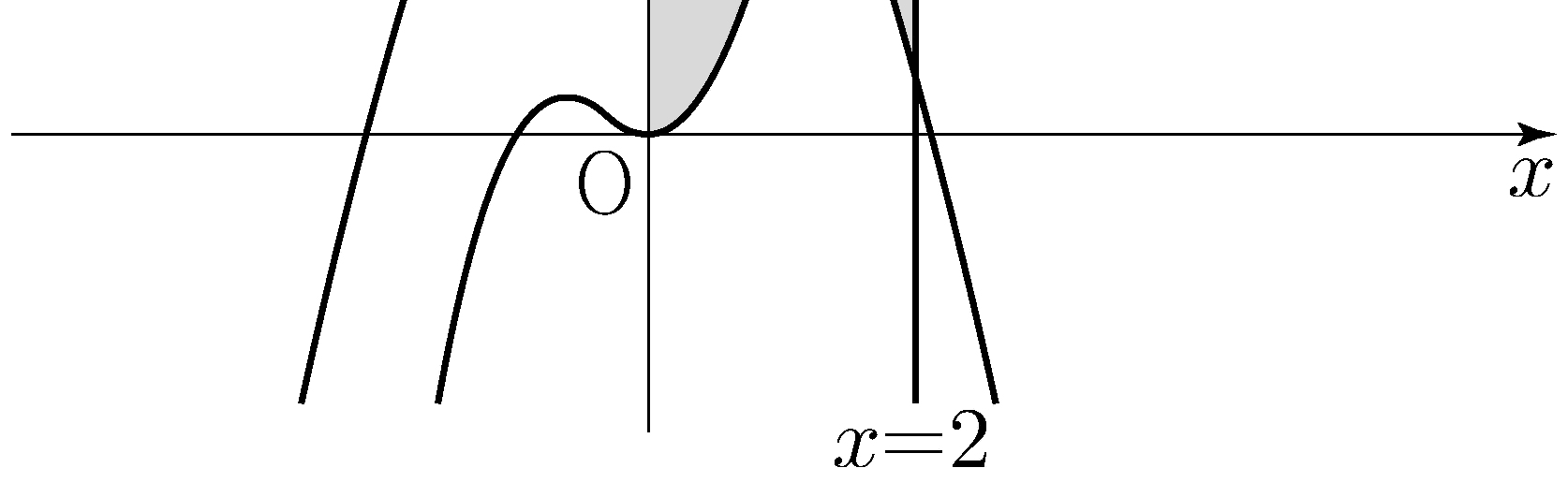
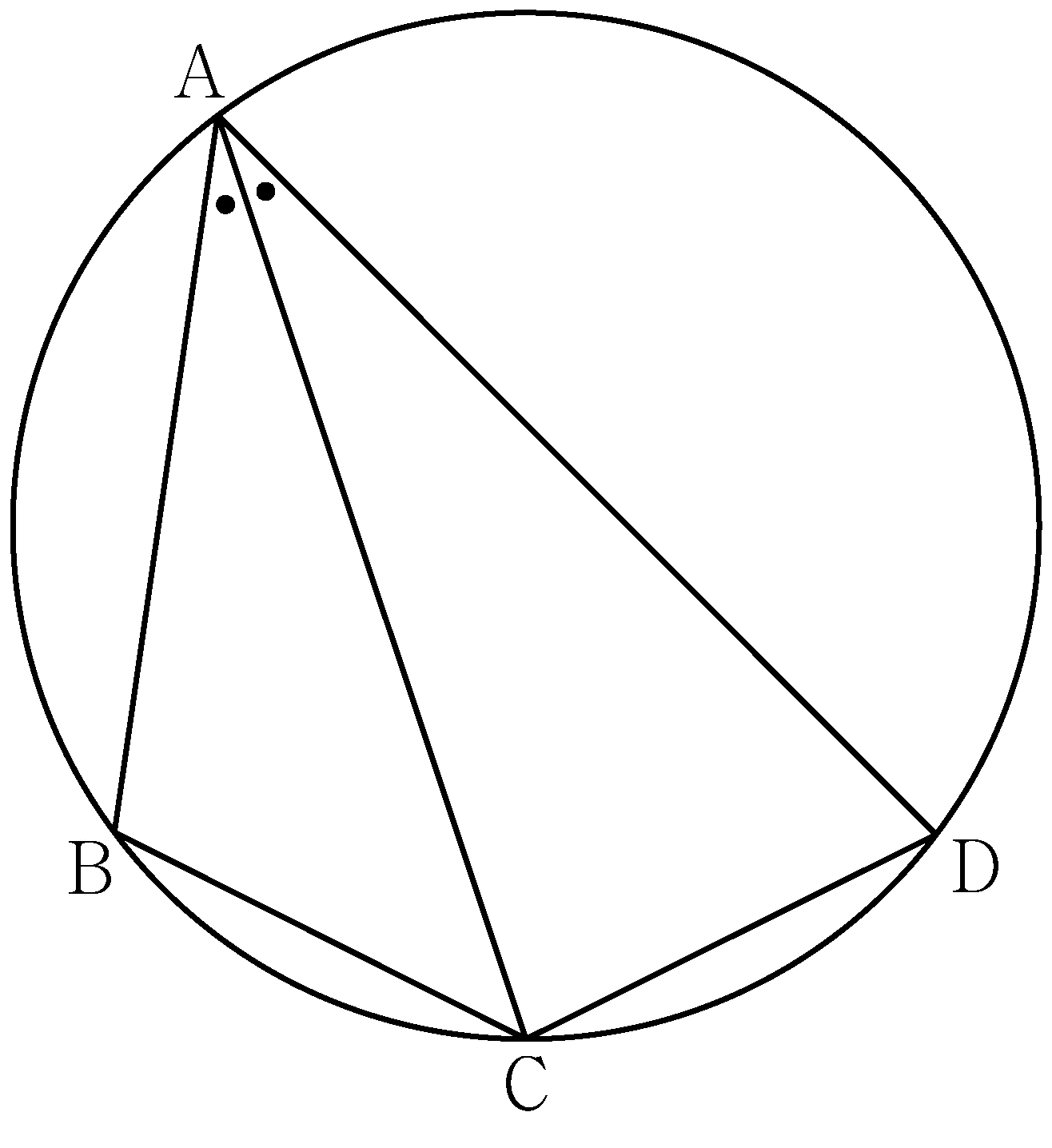
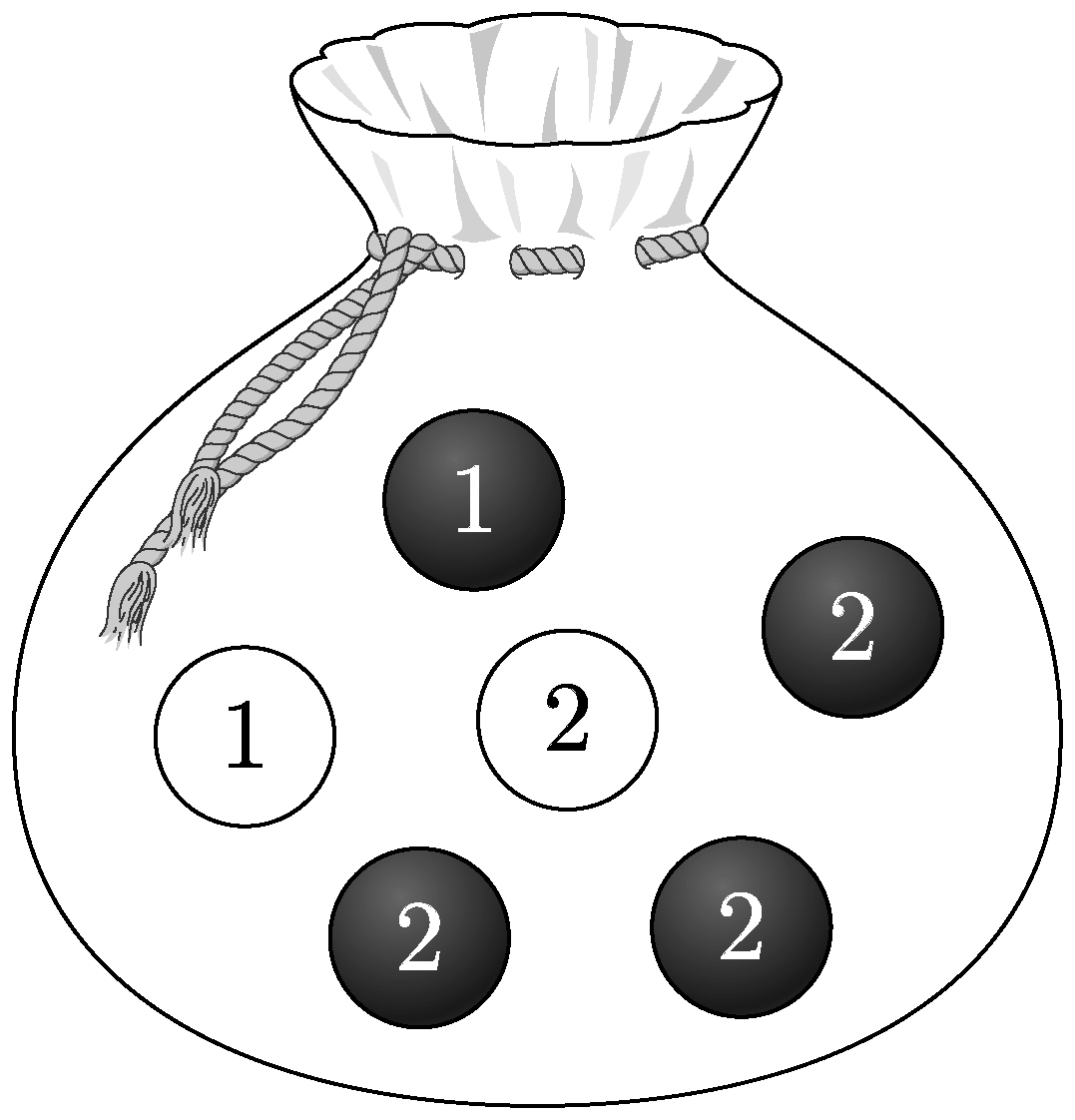
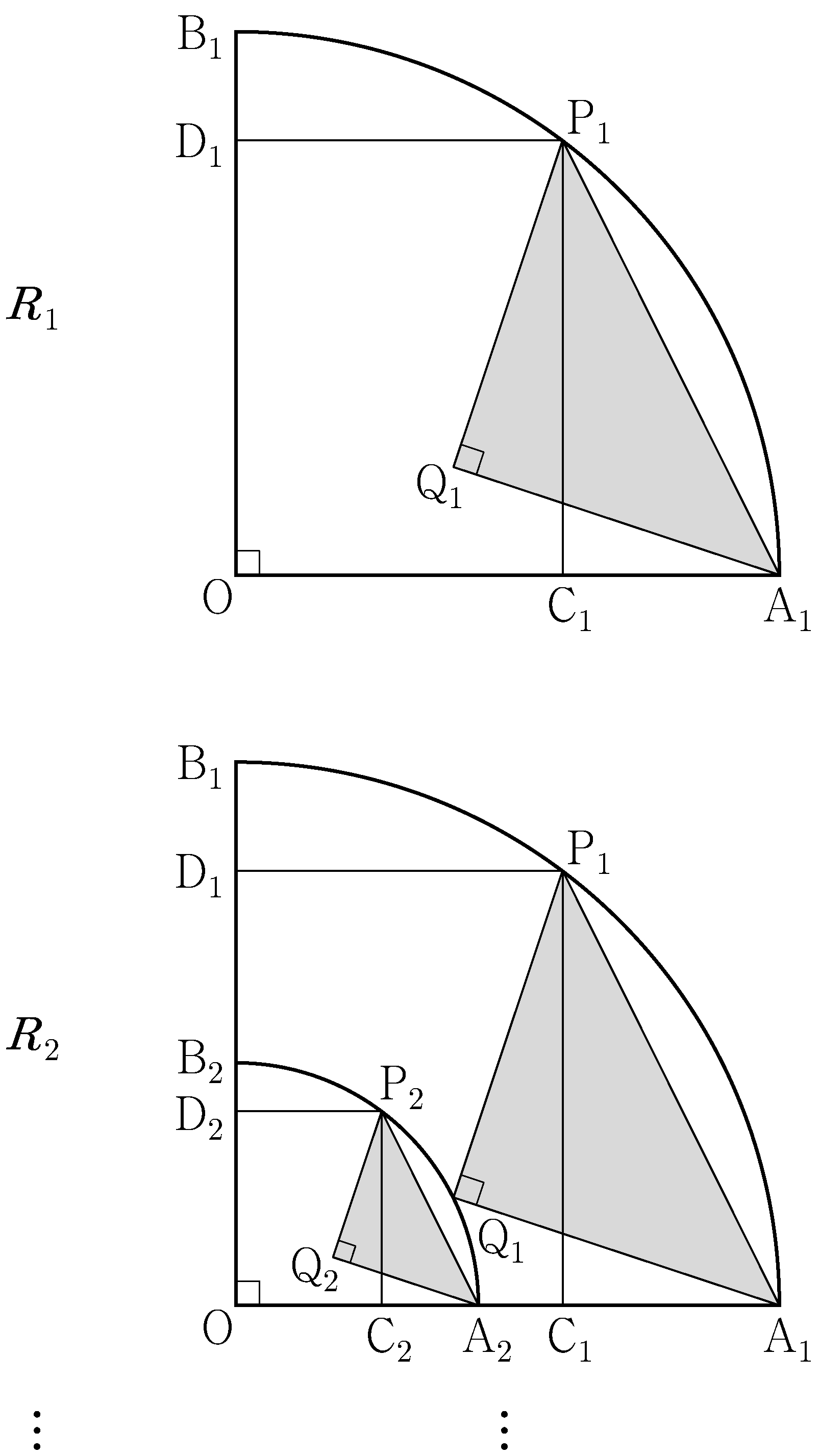
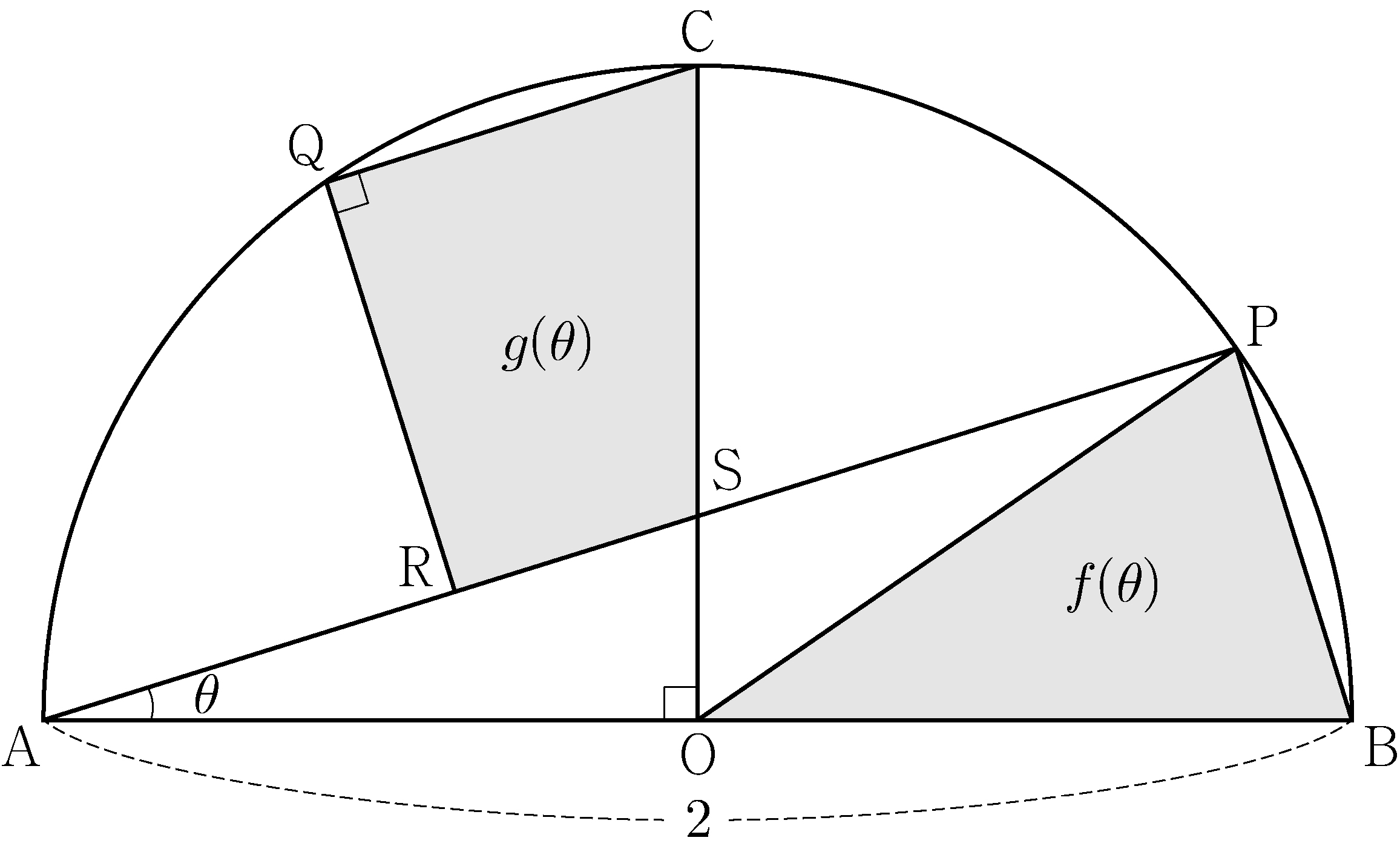
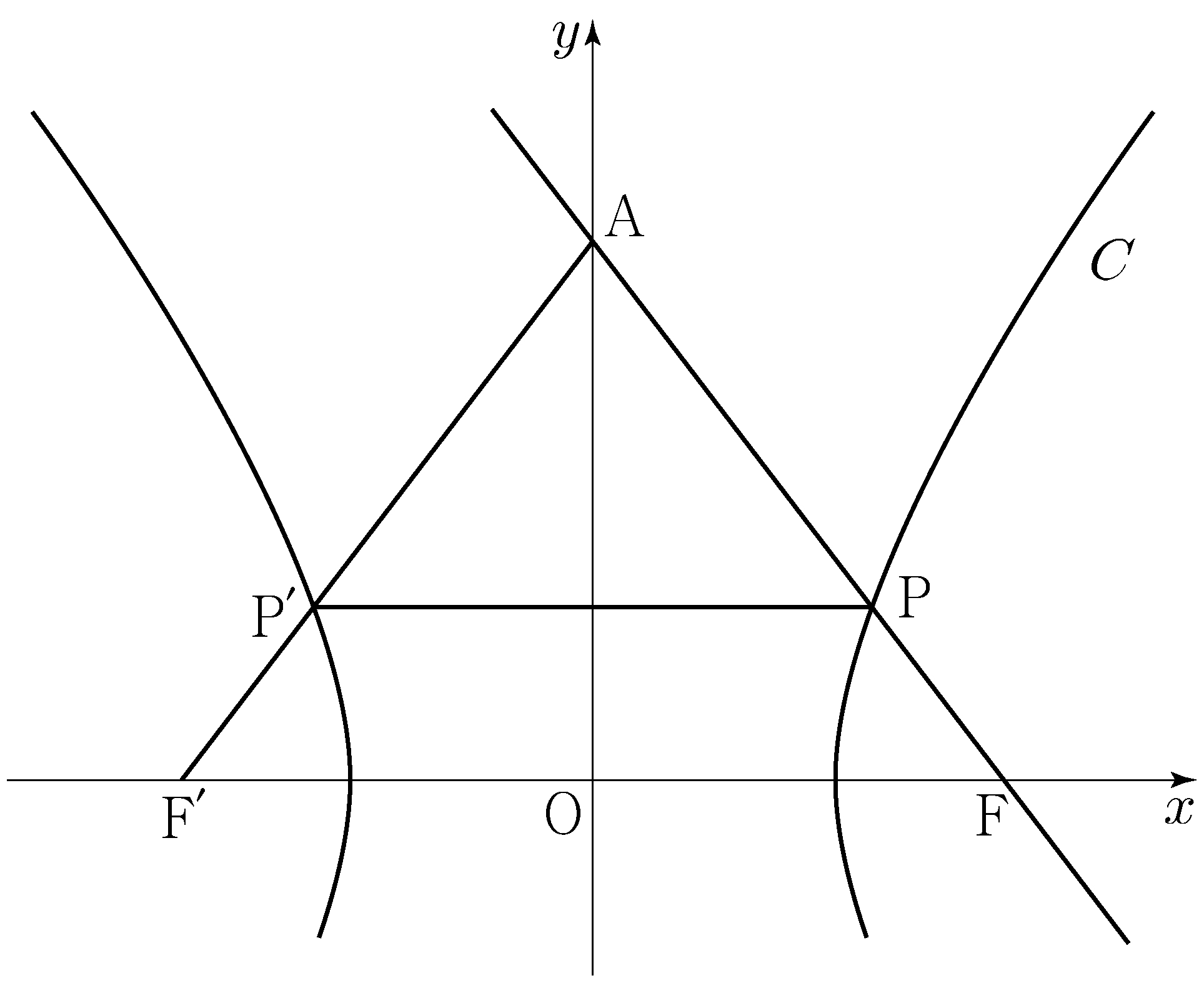
\(\dfrac{1}{4}\)
\(\dfrac{1}{2}\)
\(1\)
\(2\)
\(4\)

What is the value of \(\displaystyle\lim_{x\to\infty}\!\dfrac{\sqrt{x^2-2}+3x}{x+5}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

A geometric progression \(\{a_n\}\) with a positive common ratio satisfies

\(a_2+a_4=30\:\) and \(\:a_4+a_6=\dfrac{15}{2}\).

What is the value of \(a_1\)? [3 points]

\(48\)
\(56\)
\(64\)
\(72\)
\(80\)

For a polynomial function \(f(x)\), let \(g(x)\) be

\(g(x)=x^2f(x)\).

If \(f(2)=1\) and \(f'(2)=3\), what is the value of \(g'(2)\)? [3 points]

\(12\)
\(14\)
\(16\)
\(18\)
\(20\)

Mathematics

If \(\tan\theta<0\) and \(\cos \!\left(\! \dfrac{\pi}{2}+\theta \right)=\dfrac{\sqrt{5}}{5}\), what is the value of \(\cos\theta\)? [3 points]

\(-\dfrac{2\sqrt{5}}{5}\)
\(-\dfrac{\sqrt{5}}{5}\)
\(0\)
\(\dfrac{\sqrt{5}}{5}\)
\(\dfrac{2\sqrt{5}}{5}\)

The function \(f(x)=2x^3-9x^2+ax+5\) has a local maximum at \(x=1\), and a local minimum at \(x=b\). What is the value of \(a+b\)? (※ \(a\) and \(b\) are constants.) [3 points]

\(12\)
\(14\)
\(16\)
\(18\)
\(20\)

An arithmetic progression \(\{a_n\}\) where all terms are positive numbers and the initial term is equal to the common difference, satisfies

\(\displaystyle\sum_{k=1}^{15} \dfrac{1}{\sqrt{a_k}+\sqrt{a_{k+1}}} = 2\).

What is the value of \(a_4\)? [3 points]

\(6\)
\(7\)
\(8\)
\(9\)
\(10\)

Mathematics

What is the \(x\)-intercept of the tangent line to the curve \(y=x^3-x+2\) that passes through the point \((0,4)\)? [3 points]

\(-\dfrac{1}{2}\)
\(-1\)
\(-\dfrac{3}{2}\)
\(-2\)
\(-\dfrac{5}{2}\)

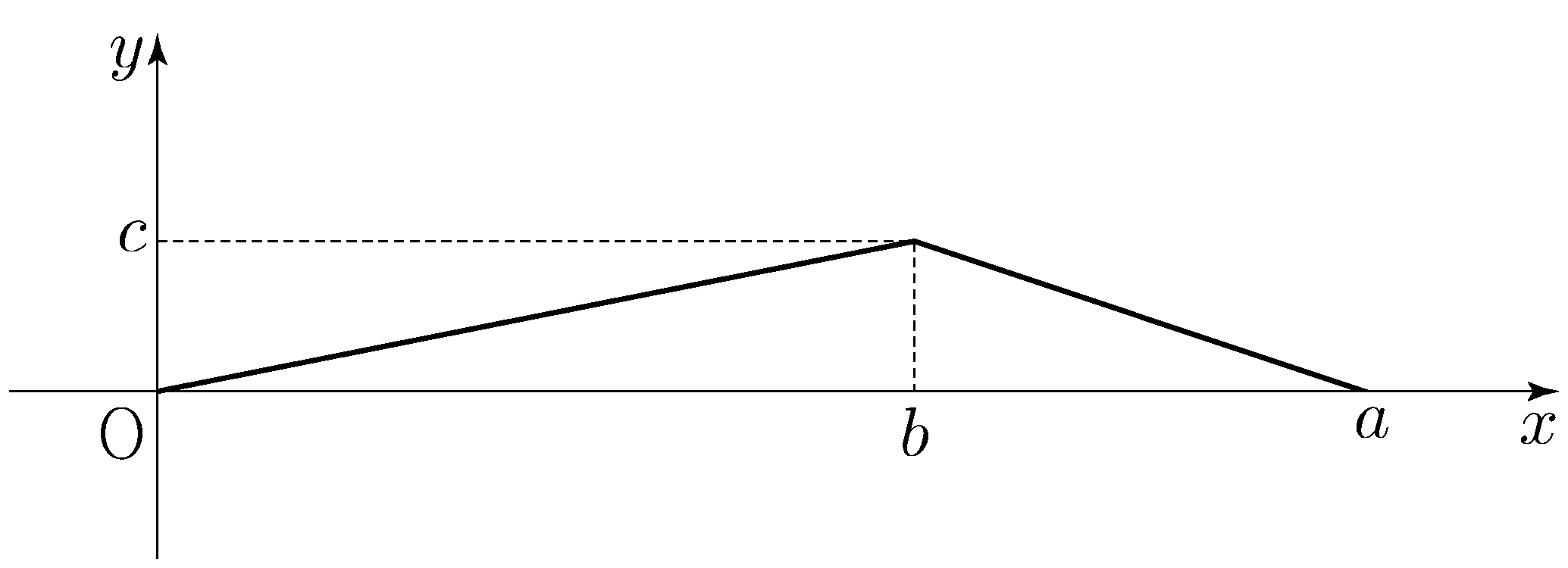
Over the closed interval \(\left[-\dfrac{\pi}{6}, b\right]\), the function

\(f(x)=a=\sqrt{3}\tan 2x\)

has a maximum value of \(7\) and a minimum value of \(3\). What is the value of \(a\times b\)? (※ \(a\) and \(b\) are constants.) [4 points]

\(\dfrac{\pi}{2}\)
\(\dfrac{5\pi}{12}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{6}\)

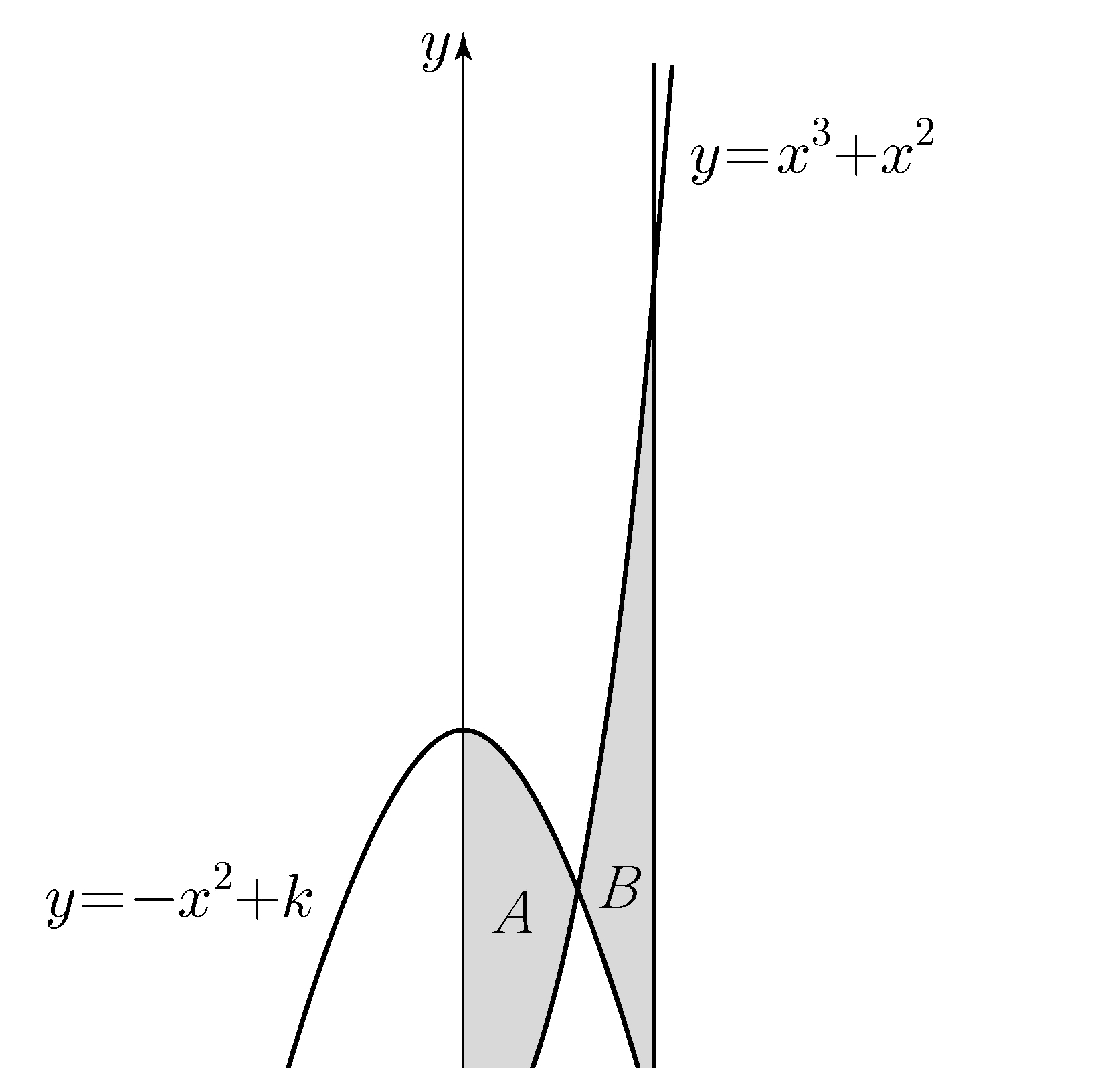
Let \(A\) be the area of the region enclosed by two curves \(y=x^3+x^2\) and \(y=-x^2+k\), and the \(y\)-axis. Let \(B\) be the area of the region enclosed by two curves \(y=x^3+x^2\) and \(y=-x^2+k\), and the line \(x=2\). If \(A=B\), what is the value of the constant \(k\)?
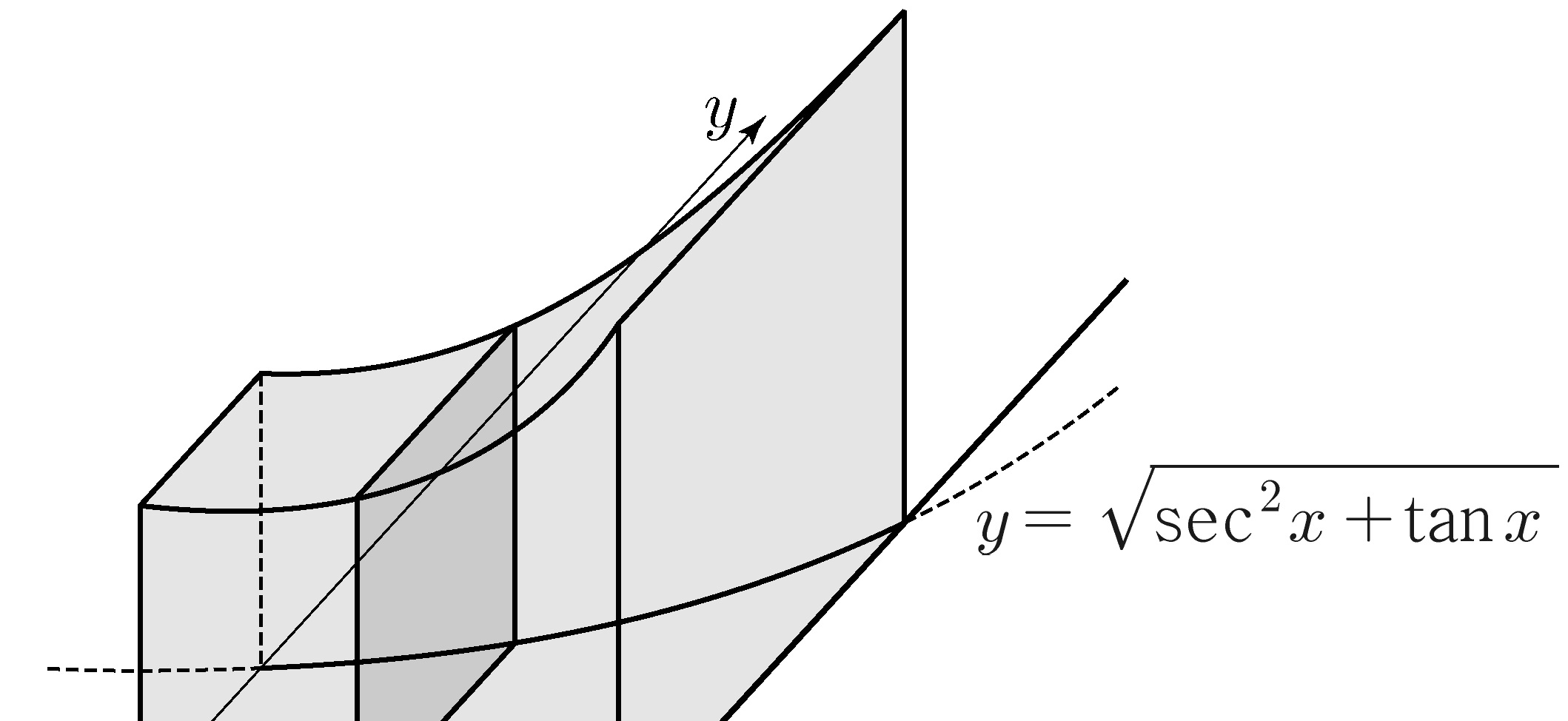
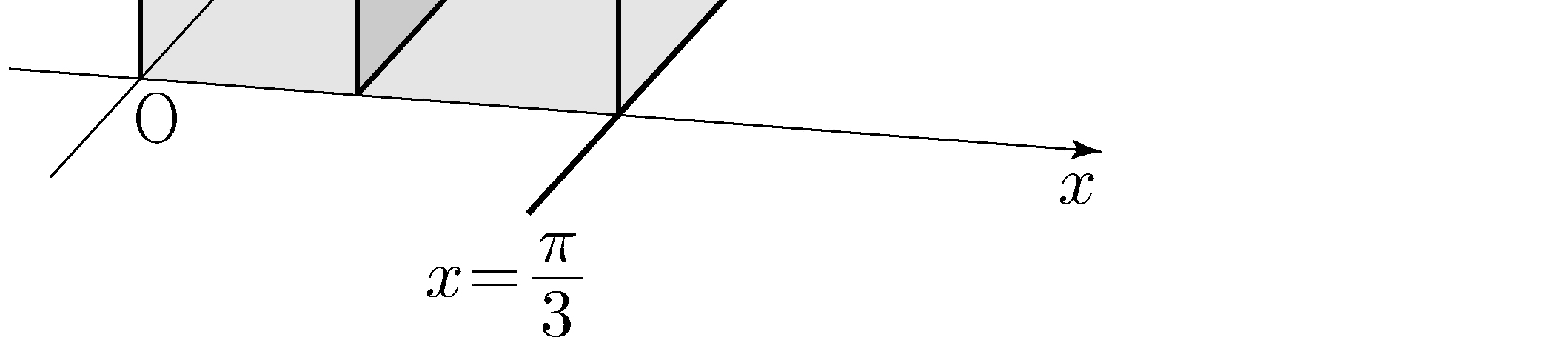
(※ \(4<k<5\)) [4 points]

\(\dfrac{25}{6}\)
\(\dfrac{13}{3}\)
\(\dfrac{9}{2}\)
\(\dfrac{14}{3}\)
\(\dfrac{29}{6}\)

Mathematics

As the figure shows, a quadrilateral \(\mathrm{ABCD}\) is inscribed in a circle and satisfies

\(\overline{\mathrm{AB}} = 5,\: \overline{\mathrm{AC}} = 3\sqrt{5},\: \overline{\mathrm{AD}} = 7\)
and \(\angle\mathrm{BAC} = \angle\mathrm{CAD}\).

What is the radius of this circle? [4 points]

\(\dfrac{5\sqrt{2}}{2}\)
\(\dfrac{8\sqrt{5}}{5}\)
\(\dfrac{5\sqrt{5}}{3}\)
\(\dfrac{8\sqrt{2}}{3}\)
\(\dfrac{9\sqrt{3}}{4}\)

A function \(f(x)\) continuous on the set of all real numbers satisfies the following.

For \(n\!-\!1\leq x \leq n\), \(|f(x)|\!=\!|6(x\!-\!n\!+\!1)(x\!-\!n)|\).
(※ This holds for all positive integers \(n\).)

A function

\(\displaystyle g(x)=\int_0^x \!f(t)dt - \int_x^4 \!f(t)dt\)

defined on the open interval \((0, 4)\), has a minimum value of \(0\) at \(x=2\). What is the value of \(\displaystyle\int_{\dfrac{1}{2}}^4 \!f(x)dx\)? [4 points]

\(-\dfrac{3}{2}\)
\(-\dfrac{1}{2}\)
\(\dfrac{1}{2}\)
\(\dfrac{3}{2}\)
\(\dfrac{5}{2}\)

Mathematics

For a positive integer \(m \, (m\geq 2)\), let \(f(m)\) be the number of positive integers \(n \, (n\geq 2)\) for which there exists an integer among the \(n\)th root of \(m^{12}\).
What is the value of \(\displaystyle\sum_{m=2}^9 f(m)\)? [4 points]

\(37\)
\(42\)
\(47\)
\(52\)
\(57\)

For a polynomial function \(f(x)\), the function \(g(x)\) is defined as follows.

\( g(x) = \begin{cases} x & \; (x<-1 \text{ or } x>1)\\ \\ f(x) & \; (-1 \leq x \leq 1) \end{cases} \)

For the function \(\displaystyle h(x)\!=\!\lim_{t\to 0+}\!g(x+t) \!\times\! \lim_{t\to 2+}\!g(x+t)\), Which option only contains every correct statement in the <List>? [4 points]

\(h(1)=3\)
\(h(x)\) is continuous on the set of all real numbers.
Suppose \(g(x)\) decreases on the closed interval \([-1,1]\) and \(g(-1)=-2\). Then \(h(x)\) has a global minimum on the set of all real numbers.

a
b
a, b
a, c
b, c

Mathematics

Among all sequences of positive integers \(\{a_n\}\) that satisfy the following condition, let \(M\) and \(m\) be the maximum value and minimum value of \(a_9\) respectively. What is the value of \(M+m\)? [4 points]

\(a_7=40\)
For all positive integers \(n\),
\(a_{n+2} \!=\! \begin{cases} a_{n+1}\!+\!a_n & (a_{n+1}\text{ is not a}\\ & \:\:\text{multiple of }3)\\ \dfrac{1}{3}a_{n+1} & (a_{n+1}\text{ is a multiple of }3) \end{cases} \)

\(216\)
\(218\)
\(220\)
\(222\)
\(224\)

Short Answer Questions

Compute the value of \(x\) for which the equation

\(\log_2 (3x+2) = 2+\log_2 (x-2)\)

is satisfied. [3 points]

A function \(f(x)\) satisfies \(f'(x)=4x^3-2x\) and \(f(0)=3\). Compute \(f(2)\). [3 points]

Mathematics

Two sequences \(\{a_n\}\) and \(\{b_n\}\) satisfy

\(\displaystyle\sum_{k=1}^5 (3a_k+5)=55 \:\) and \(\:\displaystyle\sum_{k=1}^5 (a_k+b_k)=32\).

Compute \(\displaystyle\sum_{k=1}^5 b_k\). [3 points]

Compute the number of integers \(k\) for which the equation \(2x^3-6x^2+k=0\) has \(2\) distinct positive solutions. [3 points]

A point \(\mathrm{P}\) moves on the number line, and its velocity \(v(t)\) and acceleration \(a(t)\) at time \(t\, (t\geq 0)\) satisfy the following.

For \(0\leq t\leq 2\), \(\,v(t)=2t^3-8t\).
For \(t\geq 2\), \(\,a(t)=6t+4\).

Compute the distance point \(\mathrm{P}\) travels from time \(t=0\) to \(t=3\). [4 points]

Mathematics

A function \(f(x)\) is defined as

\( f(x) = \begin{cases} \big|3^{x+2}-n\big| & \; (x < 0)\\ \\ \big|\log_2 (x+4)-n\big| & \; (x \geq 0) \end{cases} \)

where \(n\) is a positive integer. For a real number \(t\), let \(g(t)\) be the number of distinct real solutions of the equation \(f(x)=t\), solved for \(x\). Compute the sum of all positive integers \(n\) for which the maximum value of \(g(t)\) is \(4\). [4 points]

A cubic function \(f(x)\) with a leading coefficient of \(1\) and a function \(g(x)\) continuous on the set of all real numbers, satisfy the following. Compute \(f(4)\). [4 points]

\(f(x)=f(1)+(x-1)f'(g(x))\)
for all real numbers \(x\).
The minimum value of function \(g(x)\) is \(\dfrac{5}{2}\).
\(f(0)=-3\) and \(f(g(1))=6\).

2023 College Scholastic Ability Test

Mathematics (Prob. & Stat.)

Multiple Choice Questions

In the expansion of the polynomial \((x^3+3)^5\), what is the coefficient of \(x^9\)? [2 points]

\(30\)
\(60\)
\(90\)
\(120\)
\(150\)

Let us pick \(4\) of the numbers \(1, 2, 3, 4\) and \(5\), where the same number may be picked multiple times, and arrange them in a line to make a \(4\)-digit integer. Among the integers that can be made, how many are odd numbers greater than \(4000\)? [3 points]

\(125\)
\(150\)
\(175\)
\(200\)
\(225\)

Mathematics (Prob. & Stat.)

There is a box containing \(5\) white masks and \(9\) black masks. Let us randomly take out \(3\) masks from this box. What is the probability that at least one of the masks taken out is a white mask? [3 points]

\(\dfrac{8}{13}\)
\(\dfrac{17}{26}\)
\(\dfrac{9}{13}\)
\(\dfrac{19}{26}\)
\(\dfrac{10}{13}\)

There is a sack containing a white ball marked \(1\), a white ball marked \(2\), a black ball marked \(1\), and \(3\) black balls marked \(2\). Let us perform a trial of randomly taking out \(3\) balls from this sack at the same time. During this trial, let \(A\) be the event where \(1\) ball is white and \(2\) balls are black among the \(3\) balls taken out, and let \(B\) be the event where the product of \(3\) numbers marked on the \(3\) balls taken out is \(8\). What is the value of \(\mathrm{P}(A\cup B)\)? [3 points]

\(\dfrac{11}{20}\)
\(\dfrac{3}{5}\)
\(\dfrac{13}{20}\)
\(\dfrac{7}{10}\)
\(\dfrac{3}{4}\)

Mathematics (Prob. & Stat.)

The volume of one shampoo bottle produced in some company follows the normal distribution \(\mathrm{N}(m, \sigma^2)\). A \(95\%\) confidence interval for \(m\), computed with a sample of size \(16\) randomly sampled from shampoo bottles produced in this company, is \(746.1\leq m\leq 755.9\).
A \(99\%\) confidence interval for \(m\), computed with a sample of size \(n\) randomly sampled from shampoo bottles produced in this company, is \(a\leq m\leq b\). What is the minimum value of \(n\) for which \(b-a\leq 6\)?
(※ The unit of volume is \(\text{mL}\), and for a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(|Z| \leq 1.96) = 0.95\) and \(\mathrm{P}(|Z| \leq 2.58) = 0.99\).) [3 points]

\(70\)
\(74\)
\(78\)
\(82\)
\(86\)

An absolutely continuous random variable \(X\) takes the value of \(0\leq X\leq a\). The graph of the probability density function of \(X\) is as the figure shows.

Given that \(\mathrm{P}(X\leq b) - \mathrm{P}(X\geq b) = \dfrac{1}{4}\) and \(\mathrm{P}(X\leq \sqrt{5}) = \dfrac{1}{2}\), what is the value of \(a+b+c\)?
(※ \(a, b\) and \(c\) are constants.) [4 points]

\(\dfrac{11}{2}\)
\(6\)
\(\dfrac{13}{2}\)
\(7\)
\(\dfrac{15}{2}\)

Mathematics (Prob. & Stat.)

Short Answer Questions

There are \(6\) cards marked with integers from \(1\) to \(6\) on the front respectively, and all marked with the number \(0\) on the back. These cards are placed like the figure below, where integer \(k\) can be seen in the \(k\)th place for positive integers \(k\leq 6\).

Let us perform the following trial with these \(6\) cards and a die.

Throw the die once, and let \(k\) be the number it lands on. Flip the card in the \(k\)th place and put it back in position.

After repeating the trial above \(3\) times, suppose the sum of all numbers that can be seen on the \(6\) cards is even. Given this, the probability that the die landed on \(1\) exactly once is \(\dfrac{q}{p}\). Compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

For the set \(X=\{x\,|\,x\) is a positive integer \(\leq 10\}\), compute the number of functions \(f:X\to X\) that satisfy the following. [4 points]

\(f(x)\leq f(x+1)\) for all positive integers \(x\leq 9\).
\(f(x)\leq x\) for \(1\leq x \leq 5\),
and \(f(x)\geq x\) for \(6\leq x \leq 10\).
\(f(6)=f(5)+6\)

2023 College Scholastic Ability Test

Mathematics (Calculus)

Multiple Choice Questions

What is the value of \(\displaystyle\lim_{x\to 0}\dfrac{\ln(x+1)}{\sqrt{x+4}-2}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

What is the value of \(\displaystyle\lim_{n\to\infty}\!\dfrac{1}{n}\sum_{k=1}^n \sqrt{1+\dfrac{3k}{n}}\)? [3 points]

\(\dfrac{4}{3}\)
\(\dfrac{13}{9}\)
\(\dfrac{14}{9}\)
\(\dfrac{5}{3}\)
\(\dfrac{16}{9}\)

Mathematics (Calculus)

A geometric progression \(\{a_n\}\) satisfies \(\displaystyle\lim_{n\to\infty}\dfrac{a_n+1}{3^n+2^{2n-1}}=3\). What is the value of \(a_3\)? [3 points]

\(16\)
\(18\)
\(20\)
\(22\)
\(24\)

As the figure shows, there is a \(3\)-dimensional solid where one of its faces is the region enclosed by the curve \(y=\sqrt{\sec^2 x+\tan x}\) \(\left(\!0\leq x \leq \dfrac{\pi}{3}\!\right)\), the \(x\)-axis, the \(y\)-axis, and the line \(x=\dfrac{\pi}{3}\). Suppose a cross section of this solid and any plane perpendicular to the \(x\)-axis is always a square. What is the volume of this solid? [3 points]

\(\dfrac{\sqrt{3}}{2}+\dfrac{\ln2}{2}\)
\(\dfrac{\sqrt{3}}{2}+\ln2\)
\(\sqrt{3}+\dfrac{\ln2}{2}\)
\(\sqrt{3}+\ln2\)
\(\sqrt{3}+2\ln2\)

Mathematics (Calculus)

As the figure shows, there is a sector \(\mathrm{OA_1B_1}\) with center \(\mathrm{O}\), radius \(1\) and central angle \(\dfrac{\pi}{2}\). Let \(\mathrm{P_1}\) be a point on arc \(\mathrm{A_1B_1}\), \(\mathrm{C_1}\) be a point on the line segment \(\mathrm{OA_1}\), and \(\mathrm{D_1}\) be a point on the line segment \(\mathrm{OB_1}\) such that \(\mathrm{OC_1P_1D_1}\) is a rectangle and \(\overline{\mathrm{OC_1}}:\overline{\mathrm{OD_1}}=3:4\). Let \(\mathrm{Q_1}\) be a point inside the sector \(\mathrm{OA_1B_1}\) such that \(\overline{\mathrm{P_1Q_1}}=\overline{\mathrm{A_1Q_1}}\) and \(\angle\mathrm{P_1Q_1A_1}=\dfrac{\pi}{2}\). Figure \(R_1\) is obtained by coloring inside the isosceles triangle \(\mathrm{P_1Q_1A_1}\). Starting from figure \(R_1\), let \(\mathrm{A_2}\) be a point on the line segment \(\mathrm{OA_1}\) and \(\mathrm{B_2}\) be a point on the line segment \(\mathrm{OB_1}\) such that \(\overline{\mathrm{OQ_1}}=\overline{\mathrm{OA_2}}=\overline{\mathrm{OB_2}}\). Draw a sector \(\mathrm{OA_2B_2}\) with center \(\mathrm{O}\), radius \(\overline{\mathrm{OQ_1}}\) and central angle \(\dfrac{\pi}{2}\). Define four points \(\mathrm{P_2, C_2, D_2}\) and \(\mathrm{Q_2}\) with the same method used to obtain figure \(R_1\). Figure \(R_2\) is obtained by coloring inside the isosceles triangle \(\mathrm{P_2Q_2A_2}\). Continue this process, and let \(S_n\) be the area of the colored region in \(R_n\), the \(n\)th obtained figure. What is the value of \(\displaystyle\lim_{n\to\infty}S_n\)? [3 points]

\(\dfrac{9}{40}\)
\(\dfrac{1}{4}\)
\(\dfrac{11}{40}\)
\(\dfrac{3}{10}\)
\(\dfrac{13}{40}\)

As the figure shows, there is a point \(\mathrm{C}\) on a semicircle with center \(\mathrm{O}\) and the line segment \(\mathrm{AB}\) as the diameter, where \(\angle\mathrm{AOC}=\dfrac{\pi}{2}\). Let \(\mathrm{P}\) be a point on arc \(\mathrm{BC}\) and \(\mathrm{Q}\) be a point on arc \(\mathrm{CA}\) such that \(\overline{\mathrm{PB}}=\overline{\mathrm{QC}}\). Let \(\mathrm{R}\) be a point on the line segment \(\mathrm{AP}\) such that \(\angle\mathrm{CQR}=\dfrac{\pi}{2}\). Let \(\mathrm{S}\) be the intersection of line segments \(\mathrm{AP}\) and \(\mathrm{CO}\). For \(\angle\mathrm{PAB}=\theta\), let \(f(\theta)\) be the area of the triangle \(\mathrm{POB}\) and \(g(\theta)\) be the area of the quadrilateral \(\mathrm{CQRS}\). What is the value of \(\displaystyle\lim_{\theta\to 0+}\!\dfrac{3f(\theta)-2g(\theta)}{\theta^2}\)? (※ \(0<\theta<\dfrac{\pi}{4}\)) [4 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Calculus)

Short Answer Questions

For three constants \(a, b\) and \(c\), the function \(f(x)=ae^2x+be^x+c\) satisfies the following.

\(\displaystyle\lim_{x\to -\infty}\!\! \dfrac{f(x)+6}{e^x} = 1\)
\(f(\ln 2)=0\)

Let \(g(x)\) be the inverse of function \(f(x)\). Given that

\(\displaystyle\int_0^{14}g(x)dx=p+q\ln2\), compute \(p+q\).

(※ \(p\) and \(q\) are rational numbers. \(\ln2\) is irrational.) [4 points]

For a cubic function \(f(x)\) with a positive leading coefficient and the function \(g(x)=e^{\sin\pi x}-1\), the composite function \(h(x)=g(f(x))\) defined on the set of all real numbers satisfies the following.

\(h(x)\) has a local maximum value of \(0\) at \(x=0\).
On the open interval \((0, 3)\), the equation \(h(x)=1\) has \(7\) distinct real solutions.

Given that \(f(3)=\dfrac{1}{2}\) and \(f'(3)=0\), \(f(2)=\dfrac{q}{p}\). Compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

2023 College Scholastic Ability Test

Mathematics (Geometry)

Multiple Choice Questions

In \(3\)-dimensional space, consider point \(\mathrm{A}(2,2,-1)\) and its reflection about the \(x\)-axis, named point \(\mathrm{B}\). For point \(\mathrm{C}(-2,1,1)\), what is the length of the line segment \(\mathrm{BC}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

A parabola with focus \(\mathrm{F}\!\left(\!\dfrac{1}{3},0\!\right)\) and directrix \(x=-\dfrac{1}{3}\) passes through point \((a, 2)\). What is the value of \(a\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Geometry)

The tangent line to the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) at point \((2,1)\) on the ellipse, has slope \(-\dfrac{1}{2}\). What is the distance between the two foci of this ellipse?
(※ \(a\) and \(b\) are positive numbers.) [3 points]

\(2\sqrt{3}\)
\(4\)
\(2\sqrt{5}\)
\(2\sqrt{6}\)
\(2\sqrt{7}\)

Consider three vectors

\(\vec{a}=(2,4), \vec{b}=(2,8)\:\) and \(\:\vec{c}=(1,0)\)

on the \(xy\)-plane. Two vectors \(\vec{p}\) and \(\vec{q}\) satisfy

\(\big(\vec{p}-\vec{a}\big)\cdot\big(\vec{p}-\vec{b}\big)=0\:\) and \(\:\vec{q}=\dfrac{1}{2}\vec{a}+t\vec{c}\).

What is the minimum value of \(\big|\,\vec{p}-\vec{q}\,\big|\)? [3 points]

\(\dfrac{3}{2}\)
\(2\)
\(\dfrac{5}{2}\)
\(3\)
\(\dfrac{7}{2}\)

Mathematics (Geometry)

There is a plane \(\alpha\) containing line \(\mathrm{AB}\) in
\(3\)-dimensional space. For a point \(\mathrm{C}\) not on plane \(\alpha\), let \(\theta_1\) be the acute angle between line \(\mathrm{AB}\) and line \(\mathrm{AC}\). Suppose \(\sin\theta_1=\dfrac{4}{5}\), and the acute angle between line \(\mathrm{AC}\) and plane \(\alpha\) is \(\dfrac{\pi}{2}-\theta_1\). Let \(\theta_2\) be the acute angle between plane \(\mathrm{ABC}\) and plane \(\alpha\). What is the value of \(\cos\theta_2\)? [3 points]

\(\dfrac{\sqrt{7}}{4}\)
\(\dfrac{\sqrt{7}}{5}\)
\(\dfrac{\sqrt{7}}{6}\)
\(\dfrac{\sqrt{7}}{7}\)
\(\dfrac{\sqrt{7}}{8}\)

There is a point \(\mathrm{A}\) on the \(y\)-axis, and a hyperbola \(C\) with two foci \(\mathrm{F}(c, 0)\) and \(\mathrm{F'}(-c, 0)\) (\(c>0\)). Let \(\mathrm{P}\) and \(\mathrm{P'}\) be points where the hyperbola \(C\) meets the line segments \(\mathrm{AF}\) and \(\mathrm{AF'}\) respectively. If line \(\mathrm{AF}\) is parallel to an asymptote of the hyperbola \(C\), and

\(\overline{\mathrm{AP}}:\overline{\mathrm{PP'}}=5:6\:\) and \(\overline{\mathrm{PF}}=1\),

what is the length of the major axis of hyperbola \(C\)? [4 points]

\(\dfrac{13}{6}\)
\(\dfrac{9}{4}\)
\(\dfrac{7}{3}\)
\(\dfrac{29}{12}\)
\(\dfrac{5}{2}\)

Mathematics (Geometry)

Short Answer Questions

There is a trapezoid \(\mathrm{ABCD}\) on plane \(\alpha\) where \(\overline{\mathrm{AB}}=\overline{\mathrm{CD}}=\overline{\mathrm{AD}}=2\) and \(\angle\mathrm{ABC}=\angle\mathrm{BCD}=\dfrac{\pi}{3}\). For two points \(\mathrm{P}\) and \(\mathrm{Q}\) on plane \(\alpha\) that satisfy the following, compute \(\overrightarrow{\mathrm{CP}}\cdot\overrightarrow{\mathrm{DQ}}\). [4 points]

\(\overrightarrow{\mathrm{AC}}=2\big(\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{BP}}\big)\)
\(\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{PQ}}=6\)
\(2\times\angle\mathrm{BQA}=\angle\mathrm{PBQ}<\dfrac{\pi}{2}\)

There is a regular tetrahedron \(\mathrm{ABCD}\) in \(3\)-dimensional space. Let \(S\) be a sphere that passes through point \(\mathrm{B}\) whose center is the circumcenter of the equilateral triangle \(\mathrm{BCD}\).
Let \(\mathrm{P}\), \(\mathrm{Q}\) and \(\mathrm{R}\) be points where the sphere \(S\) meets the line segments \(\mathrm{AB}\), \(\mathrm{AC}\) and \(\mathrm{AD}\) respectively
(\(\mathrm{P} \ne \mathrm{B}\), \(\mathrm{Q} \ne \mathrm{C}\) and \(\mathrm{R} \ne \mathrm{D}\)).
Let \(\alpha\) be a plane tangent to the sphere \(S\) at point \(\mathrm{P}\). If the radius of sphere \(S\) is \(6\), the projection of triangle \(\mathrm{PQR}\) onto plane \(\alpha\) has an area of \(k\). Compute \(k^2\). [4 points]