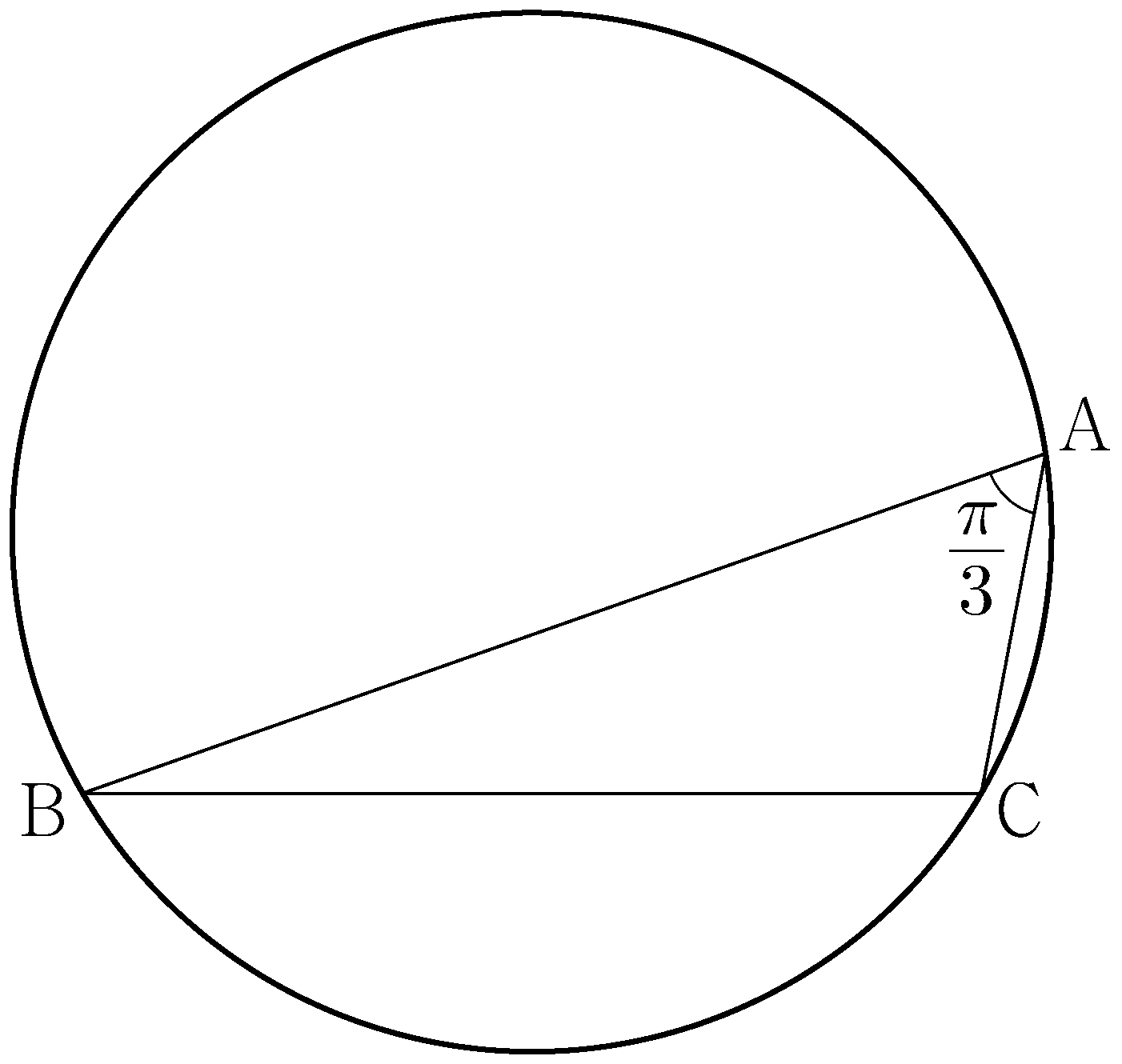
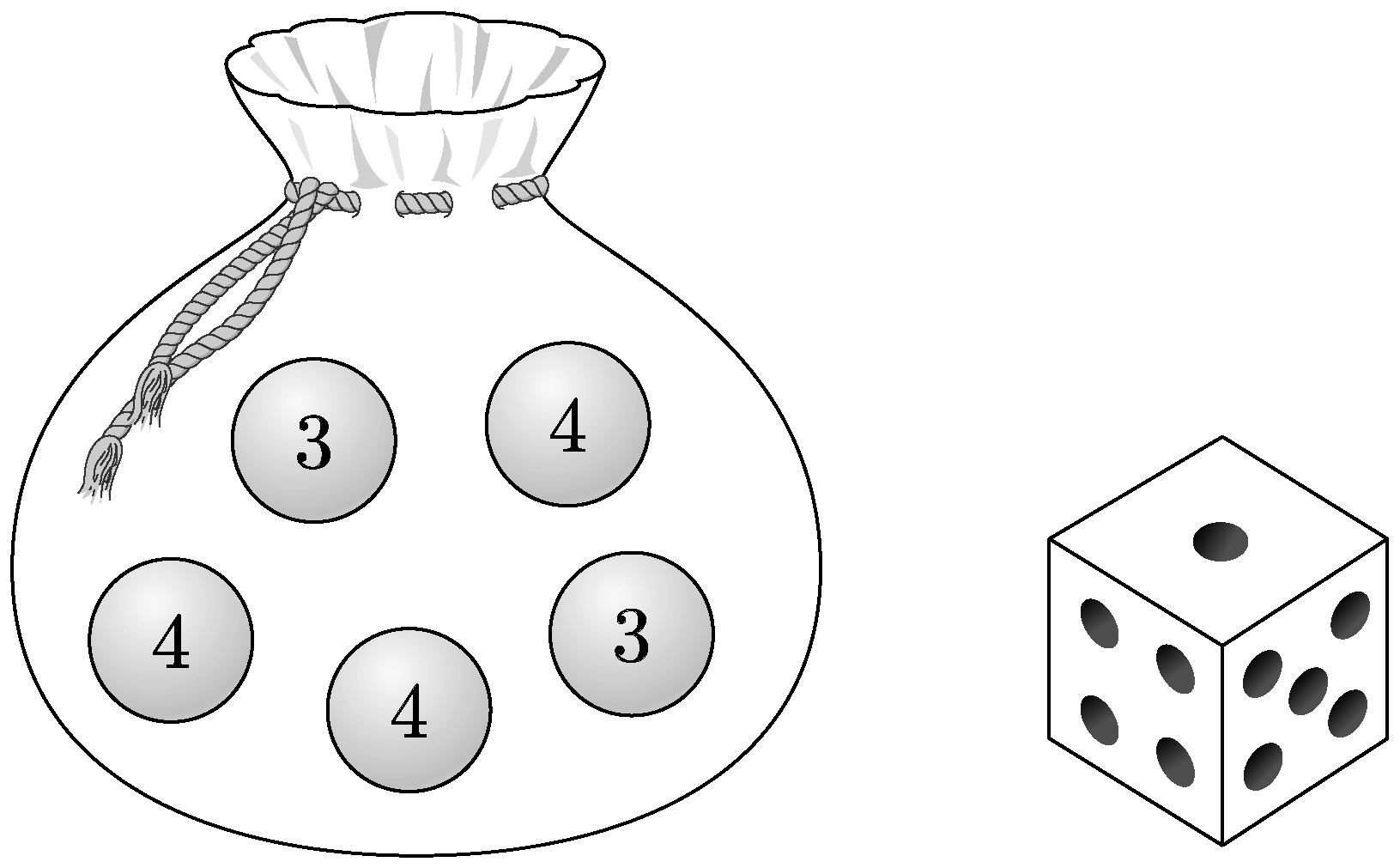
- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)
Mathematics (Type Na)
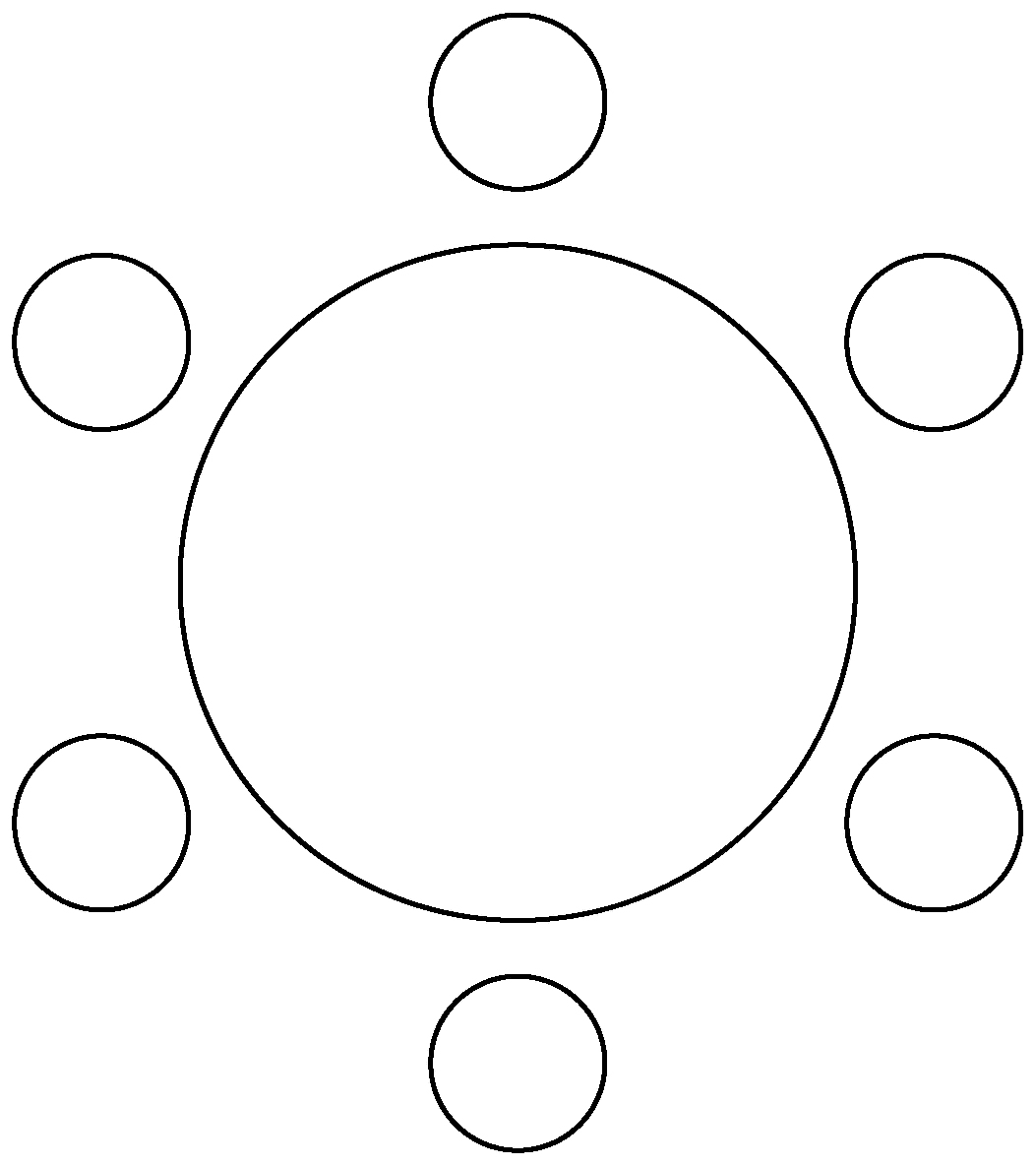
(※ If rotating one case results in another case, the two are not considered distinct.) [4 points]
- \(\mathrm{A}\) and \(\mathrm{B}\) are adjacent.
- \(\mathrm{B}\) and \(\mathrm{C}\) are not adjacent.
- \(32\)
- \(34\)
- \(36\)
- \(38\)
- \(40\)
\(4\sin^2 x-4\cos\!\left(\!\dfrac{\pi}{2}+x\!\right)-3=0\)
where \(0\leq x <4\pi\)?
[4 points]
- \(5\pi\)
- \(6\pi\)
- \(7\pi\)
- \(8\pi\)
- \(9\pi\)