2021 College Scholastic Ability Test

Mathematics (Type Ga)

Multiple Choice Questions
What is the value of \(\sqrt[3]{9}\times3^{^1/_3}\)? [2 points]
  1. \(1\)
  2. \(3^{^1/_2}\)
  3. \(3\)
  4. \(3^{^3/_2}\)
  5. \(9\)
What is the value of \(\displaystyle\lim_{n\to\infty} \dfrac{1}{\sqrt{4n^2+2n+1}-2n}\)? [2 points]
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)
Suppose \(\dfrac{\pi}{2}<\theta<\pi\). If \(\sin\theta=\dfrac{\sqrt{21}}{7}\), what is the value of \(\tan\theta\)? [2 points]
  1. \(-\dfrac{\sqrt{3}}{2}\)
  2. \(-\dfrac{\sqrt{3}}{4}\)
  3. \(0\)
  4. \(\dfrac{\sqrt{3}}{4}\)
  5. \(\dfrac{\sqrt{3}}{2}\)
Two events \(A\) and \(B\) satisfy
\(\mathrm{P}(B|A) = \dfrac{1}{4}, \: \mathrm{P}(A|B) = \dfrac{1}{3}\)
and \(\: \mathrm{P}(A)+\mathrm{P}(B) = \dfrac{7}{10}\).
What is the value of \(\mathrm{P}(A\cap B)\)? [3 points]
  1. \(\dfrac{1}{7}\)
  2. \(\dfrac{1}{8}\)
  3. \(\dfrac{1}{9}\)
  4. \(\dfrac{1}{10}\)
  5. \(\dfrac{1}{11}\)

Mathematics (Type Ga)

What is the number of positive integers \(x\) that satisfy the inequality \(\left(\!\dfrac{1}{9}\!\right)^{\!x}<3^{21-4x}\)? [3 points]
  1. \(6\)
  2. \(7\)
  3. \(8\)
  4. \(9\)
  5. \(10\)
Let \(\overline{X}\) be the mean of a sample of size \(16\) randomly sampled from a population following the normal distribution \(\mathrm{N}(20,5^2)\). What is the value of \(\mathrm{E}(\overline{X})+\sigma(\overline{X})\)? [3 points]
  1. \(\dfrac{83}{4}\)
  2. \(\dfrac{85}{4}\)
  3. \(\dfrac{87}{4}\)
  4. \(\dfrac{89}{4}\)
  5. \(\dfrac{91}{4}\)
Let \(a\) and \(b\) be the local maximum and minimum value of the function \(f(x)=(x^2-2x-7)e^x\) respectively. What is the value of \(a\times b\)? [3 points]
  1. \(-32\)
  2. \(-30\)
  3. \(-28\)
  4. \(-26\)
  5. \(-24\)

Mathematics (Type Ga)

What is the area of the region enclosed by the curve \(y=e^{2x}\), the \(x\)-axis, and two lines \(x=\ln\dfrac{1}{2}\) and \(x=\ln2\)? [3 points]
  1. \(\dfrac{5}{3}\)
  2. \(\dfrac{15}{8}\)
  3. \(\dfrac{15}{7}\)
  4. \(\dfrac{5}{2}\)
  5. \(3\)
There are \(5\) cards marked with letters \(\mathrm{A,B,C,D}\) and \(\mathrm{E}\) respectively, and \(4\) cards marked with numbers \(1,2,3\) and \(4\) respectively. Suppose we randomly arrange these \(9\) cards in a line, using each card once. What is the probability that the card marked with the letter \(\mathrm{A}\) has cards marked with numbers directly to its right and to its left? [3 points]
  1. \(\dfrac{5}{12}\)
  2. \(\dfrac{1}{3}\)
  3. \(\dfrac{1}{4}\)
  4. \(\dfrac{1}{6}\)
  5. \(\dfrac{1}{12}\)
Consider a triangle \(\mathrm{ABC}\) where \(\angle\mathrm{A}=\dfrac{\pi}{3}\) and \(\overline{\mathrm{AB}}:\overline{\mathrm{AC}}=3:1\). If the circumcircle of the triangle \(\mathrm{ABC}\) has a radius of \(7\), what is the length of the line segment \(\mathrm{AC}\)? [3 points]
  1. \(2\sqrt{5}\)
  2. \(\sqrt{21}\)
  3. \(\sqrt{22}\)
  4. \(\sqrt{23}\)
  5. \(2\sqrt{6}\)

Mathematics (Type Ga)

What is the value of \(\displaystyle\lim_{n\to\infty}\!\dfrac{1}{n} \sum_{k=1}^n\sqrt{\dfrac{3n}{3n+k}}\)? [3 points]
  1. \(4\sqrt{3}-6\)
  2. \(\sqrt{3}-1\)
  3. \(5\sqrt{3}-8\)
  4. \(2\sqrt{3}-3\)
  5. \(3\sqrt{3}-5\)
A random variable \(X\) follows a normal distribution with a mean of \(8\) and a standard deviation of \(3\), and a random variable \(Y\) follows a normal distribution with a mean of \(m\) and a standard deviation of \(\sigma\). Two random variables \(X\) and \(Y\) satisfy
\(\mathrm{P}(4\leq X\leq 8)+\mathrm{P}(Y\geq 8)=\dfrac{1}{2}\).
What is the value of \(\mathrm{P}\!\left(\!Y\leq 8+\dfrac{2\sigma}{3}\!\right)\) computed using the standard normal table to the right? [3 points]
\(z\)\(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\)
\(1.0\)\(0.3413\)
\(1.5\)\(0.4332\)
\(2.0\)\(0.4772\)
\(2.5\)\(0.4938\)
  1. \(0.8351\)
  2. \(0.8413\)
  3. \(0.9332\)
  4. \(0.9772\)
  5. \(0.9938\)

Mathematics (Type Ga)

For a real number \(a\) in \(\dfrac{1}{4}<a<1\), let \(\mathrm{A}\) and \(\mathrm{B}\) be points where the line \(y=1\) meets the two curves \(y=\log_a x\) and \(y=\log_{4a} x\) respectively, and let \(\mathrm{C}\) and \(\mathrm{D}\) be points where the line \(y=-1\) meets the two curves \(y=\log_a x\) and \(y=\log_{4a} x\) respectively.
Which option only contains every correct statement in the <List>? [3 points]
  1. The point externally dividing the line segment \(\mathrm{AB}\) in the ratio \(1:4\) has coordinates \((0,1)\).
  2. If the quadrilateral \(\mathrm{ABCD}\) is a rectangle,
    then \(a=\dfrac{1}{2}\).
  3. If \(\overline{\mathrm{AB}}<\overline{\mathrm{CD}}\), then \(\dfrac{1}{2}<a<1\).
  1. a
  2. c
  3. a, b
  4. b, c
  5. a, b, c
As the figure shows, there is a rectangle \(\mathrm{AB_1C_1D_1}\) where \(\overline{\mathrm{AB_1}}=2\) and \(\overline{\mathrm{AD_1}}=4\). Let \(\mathrm{E_1}\) be the point internally dividing the line segment \(\mathrm{AD_1}\) in the ratio \(3:1\). Let \(\mathrm{F_1}\) be a point inside the rectangle \(\mathrm{AB_1C_1D_1}\) such that \(\overline{\mathrm{F_1E_1}}=\overline{\mathrm{F_1C_1}}\) and \(\angle\mathrm{E_1F_1C_1}=\dfrac{\pi}{2}\).
Figure \(R_1\) is obtained by drawing the triangle \(\mathrm{E_1F_1C_1}\) and coloring inside the quadrilateral \(\mathrm{E_1F_1C_1D_1}\).
Starting from figure \(R_1\), draw a rectangle \(\mathrm{AB_2C_2D_2}\) where \(\mathrm{B_2, C_2}\) and \(\mathrm{D_2}\) are points on line segments \(\mathrm{AB_1, E_1F_1}\) and \(\mathrm{AE_1}\) respectively, and \(\overline{\mathrm{AB_2}}:\overline{\mathrm{AD_2}}=1:2\). With the same method used to obtain figure \(R_1\), figure \(R_2\) is obtained by drawing the triangle \(\mathrm{E_2F_2C_2}\) and coloring inside the quadrilateral \(\mathrm{E_2F_2C_2D_2}\). Continue this process, and let \(S_n\) be the area of the colored region in \(R_n\), the \(n\)th obtained figure. What is the value of \(\displaystyle\lim_{n\to\infty}S_n\)? [4 points]
  1. \(\dfrac{441}{103}\)
  2. \(\dfrac{441}{109}\)
  3. \(\dfrac{441}{115}\)
  4. \(\dfrac{441}{121}\)
  5. \(\dfrac{441}{127}\)

Mathematics (Type Ga)

A function \(f(x)\) differentiable on \(x>0\) satisfies
\(f'(x)=2-\dfrac{3}{x^2}\:\) and \(\:f(1)=5\).
If a function \(g(x)\) differentiable on \(x<0\) satisfies the following, what is the value of \(g(-3)\)? [4 points]
  1. \(g'(x)=f'(-x)\) for all \(x<0\).
  2. \(f(2)+g(-2)=9\)
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)
For a constant \(k\,(k>1)\), consider a sequence \(\{a_n\}\) that satisfies the following.
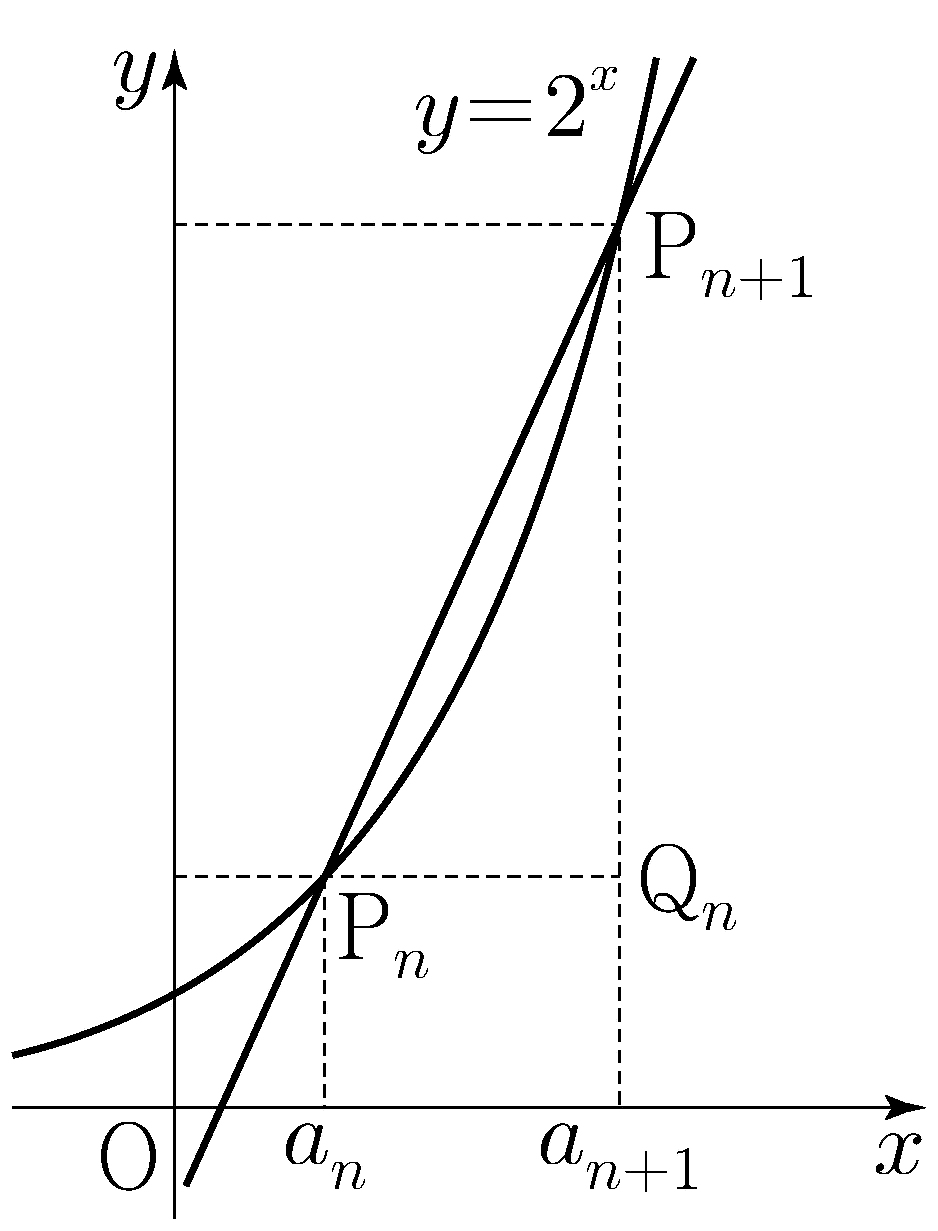
\(a_n<a_{n+1}\) for all positive integers \(n\),
and a line passing through points \(\mathrm{P}_n\big(a_n,2^{a_n}\big)\) and \(\mathrm{P}_{n+1}\big(a_{n+1},2^{a_{n+1}}\big)\) has a slope of \(k\times 2^{a_n}\).
Let \(\mathrm{Q_n}\) be the point where a horizontal line through \(\mathrm{P}_n\) meets a vertical line through \(\mathrm{P}_{n+1}\). Let \(A_n\) be the area of the triangle \(\mathrm{P}_n\mathrm{Q}_n\mathrm{P}_{n+1}\).
Given that \(a_1=1\) and \(\dfrac{A_3}{A_1}=16\),
the following is a process computing \(A_n\).
A line passing through points \(\mathrm{P}_n\) and \(\mathrm{P}_{n+1}\) has a slope of \(k\times 2^{a_n}\), so
\(2^{a_{n+1}-a_n}=k(a_{n+1}-a_n)+1\).
In other words, \(a_{n+1}-a_n\) is a solution to the equation \(2^x=kx+1\) for all positive integers \(n\).
Since \(k>1\), the equation \(2^x=kx+1\) only has one positive solution \(d\). Therefore \(a_{n+1}-a_n=d\) for all \(n\), so \(\{a_n\}\) is an arithmetic progression with a common difference of \(d\).
Since point \(\mathrm{Q_n}\) has coordinates \(\big(a_n+1,2^{a_n}\big)\),
\(A_n=\dfrac{1}{2}(a_{n+1}-a_n)\big(2^{a_{n+1}}-2^{a_n}\big)\).
Since \(\dfrac{A_3}{A_1}=16\), \(d=\fbox{\(\;(\alpha)\;\)}\),
and the general term of the sequence \(\{a_n\}\) is
\(a_n=\fbox{\(\;(\beta)\;\)}\).
Therefore \(A_n=\fbox{\(\;(\gamma)\;\)}\) for all positive integers \(n\).
Let \(p\), be the correct number for \((\alpha)\), and let \(f(n)\) and \(g(n)\) be the correct expression for \((\beta)\) and \((\gamma)\) respectively. What is the value of \(p+\dfrac{g(4)}{f(2)}\)? [4 points]
  1. \(118\)
  2. \(121\)
  3. \(124\)
  4. \(127\)
  5. \(130\)

Mathematics (Type Ga)

Suppose a point \(\mathrm{P}\) is on the origin of an \(xy\)-plane. Let us perform the following trial using a die.
Throw the die once.
If the result is \(2\) or less, move point \(\mathrm{P}\) by \(3\) towards the positive direction of the \(x\)-axis.
If the result is \(3\) or more, move point \(\mathrm{P}\) by \(1\) towards the positive direction of the \(y\)-axis.
Let a random variable \(X\) be the distance between point \(\mathrm{P}\) and the line \(3x+4y=0\) after the trial above was repeated \(15\) times. What is the value of \(\mathrm{E}(X)\)? [4 points]
  1. \(13\)
  2. \(15\)
  3. \(17\)
  4. \(19\)
  5. \(21\)
For a real number \(a\), define the function \(f(x)\) as
\(\displaystyle f(x)=\lim_{n\to\infty}\dfrac{(a-2)x^{2n+1}+2x}{3x^{2n}+1}\).
What is the sum of all values of \(a\) for which \((f\circ f)(1)=\dfrac{5}{4}\)? [4 points]
  1. \(\dfrac{11}{2}\)
  2. \(\dfrac{13}{2}\)
  3. \(\dfrac{15}{2}\)
  4. \(\dfrac{17}{2}\)
  5. \(\dfrac{19}{2}\)

Mathematics (Type Ga)

There is a sack containing \(5\) balls marked with numbers \(3,3,4,4\) and \(4\) respectively. Let us perform the following trial and set a score using this sack and a die.
Randomly take out a ball from the sack.
If the number marked on the ball taken out is \(3\), throw the die \(3\) times and set the score as the sum of the three numbers it lands on.
If the number marked on the ball taken out is \(4\), throw the die \(4\) times and set the score as the sum of the four numbers it lands on.
What is the probability that the score set by performing this trial once is \(10\)? [4 points]
  1. \(\dfrac{13}{180}\)
  2. \(\dfrac{41}{540}\)
  3. \(\dfrac{43}{540}\)
  4. \(\dfrac{1}{12}\)
  5. \(\dfrac{47}{540}\)
Consider the function \(f(x)=\pi\sin2\pi x\). A positive integer \(n\) and a function \(g(x)\) defined on the set of all real numbers whose image is the set \(\{0,1\}\) satisfy the following. What is the value of \(n\)? [4 points]
The function \(h(x)=f(nx)g(x)\) is continuous on the set of all real numbers, and
\(\displaystyle\int_{-1}^1 h(x)dx=2\) and \(\displaystyle\int_{-1}^1 xh(x)dx=-\dfrac{1}{32}\).
  1. \(8\)
  2. \(10\)
  3. \(12\)
  4. \(14\)
  5. \(16\)

Mathematics (Type Ga)

A sequence \(\{a_n\}\) satisfies \(0<a_1<1\), and the following for all positive integers \(n\).
  1. \(a_{2n}=a_2\times a_n+1\)
  2. \(a_{2n+1}=a_2\times a_n-2\)
If \(a_8-a_{15}=63\), what is the value of \(\dfrac{a_8}{a_1}\)? [4 points]
  1. \(91\)
  2. \(92\)
  3. \(93\)
  4. \(94\)
  5. \(95\)
Short Answer Questions
In the expansion of \(\left(\!x+\dfrac{3}{x^2}\!\right)^{\!5}\), compute the coefficient of \(x^2\). [3 points]
For the function \(f(x)=\dfrac{x^2-2x-6}{x-1}\),
compute \(f'(0)\). [3 points]

Mathematics (Type Ga)

As the figure shows, there is a right triangle \(\mathrm{ABC}\) where \(\overline{\mathrm{AB}}=2\) and \(\angle\mathrm{B}=\dfrac{\pi}{2}\). Let \(\mathrm{D}\) and \(\mathrm{E}\) be points where the circle with center \(\mathrm{A}\) and radius \(1\) meets the line segments \(\mathrm{AB}\) and \(\mathrm{AC}\) respectively.
Let \(\mathrm{F}\) be one of the points that trisect the arc \(\mathrm{DE}\) that is closer to point \(\mathrm{D}\). Let \(\mathrm{G}\) be the point where the line \(\mathrm{AF}\) meets the line segment \(\mathrm{BC}\).
For \(\angle\mathrm{BAG}=\theta\), let \(f(\theta)\) be the area of the common region inside triangle \(\mathrm{ABG}\) and outside sector \(\mathrm{ADF}\), and let \(g(\theta)\) be the area of the sector \(\mathrm{AFE}\).
Compute \(\displaystyle40\times\lim_{\theta\to0+}\!\dfrac{f(\theta)}{g(\theta)}\). (※ \(0<\theta<\dfrac{\pi}{6}\)) [3 points]
An arithmetic progression \(\{a_n\}\) with an initial term of \(3\) satisfies \(\displaystyle\sum_{k=1}^5 a_k=55\). Compute \(\displaystyle\sum_{k=1}^5 k(a_k-3)\). [3 points]
There are \(6\) students including three students \(\mathrm{A, B}\) and \(\mathrm{C}\). Compute the number of ways for these \(6\) students to sit around a circular table in equal distances while satisfying the following.
(※ If rotating one case results in another case, the two are not considered distinct.) [4 points]
  1. \(\mathrm{A}\) and \(\mathrm{B}\) are adjacent.
  2. \(\mathrm{B}\) and \(\mathrm{C}\) are not adjacent.

Mathematics (Type Ga)

Compute the number of positive integers \(n\) for which the value of \(\log_4 2n^2-\dfrac{1}{2}\log_2\sqrt{n}\) is a positive integer less than or equal to \(40\). [4 points]
For two constants \(a\) and \(b\) \((a<b)\), define the function \(f(x)\) as
\(f(x)=(x-a)(x-b)^2\).
For the function \(g(x)=x^3+x+1\) and its inverse \(g^{-1}(x)\), the composite function \(h(x)=\big(f\circ g^{-1}\big)(x)\) satisfies the following. Compute \(f(8)\). [4 points]
  1. The function \((x-1)|h(x)|\) is differentiable on the set of all real numbers.
  2. \(h'(3)=2\)

Mathematics (Type Ga)

There are \(6\) black hats and \(6\) white hats. Compute the number of ways to distribute all of the hats to four students \(\mathrm{A,B,C}\) and \(\mathrm{D}\) according to the following rules. (※ Hats of the same color are not considered distinct.) [4 points]
  1. Each student receives at least \(1\) hat.
  2. Student \(\mathrm{A}\) receives at least \(4\) black hats.
  3. There are exactly \(2\) students who receive more black hats than white hats, and student \(\mathrm{A}\) is one of them.
For a cubic function \(f(x)\) with a leading coefficient of \(1\), the function \(g(x)=f\big(\sin^2\pi x\big)\) defined on the set of all real numbers satisfies the following.
  1. There are \(3\) values of \(x\) in \(0<x<1\) where the function \(g(x)\) has a local maximum, and these local maximum values are all equal.
  2. \(g(x)\) has a global maximum value of \(\dfrac{1}{2}\) and a global minimum value of \(0\).
Given that \(f(2)=a+b\sqrt{2}\), compute \(a^2+b^2\).
(※ \(a\) and \(b\) are rational numbers.) [4 points]