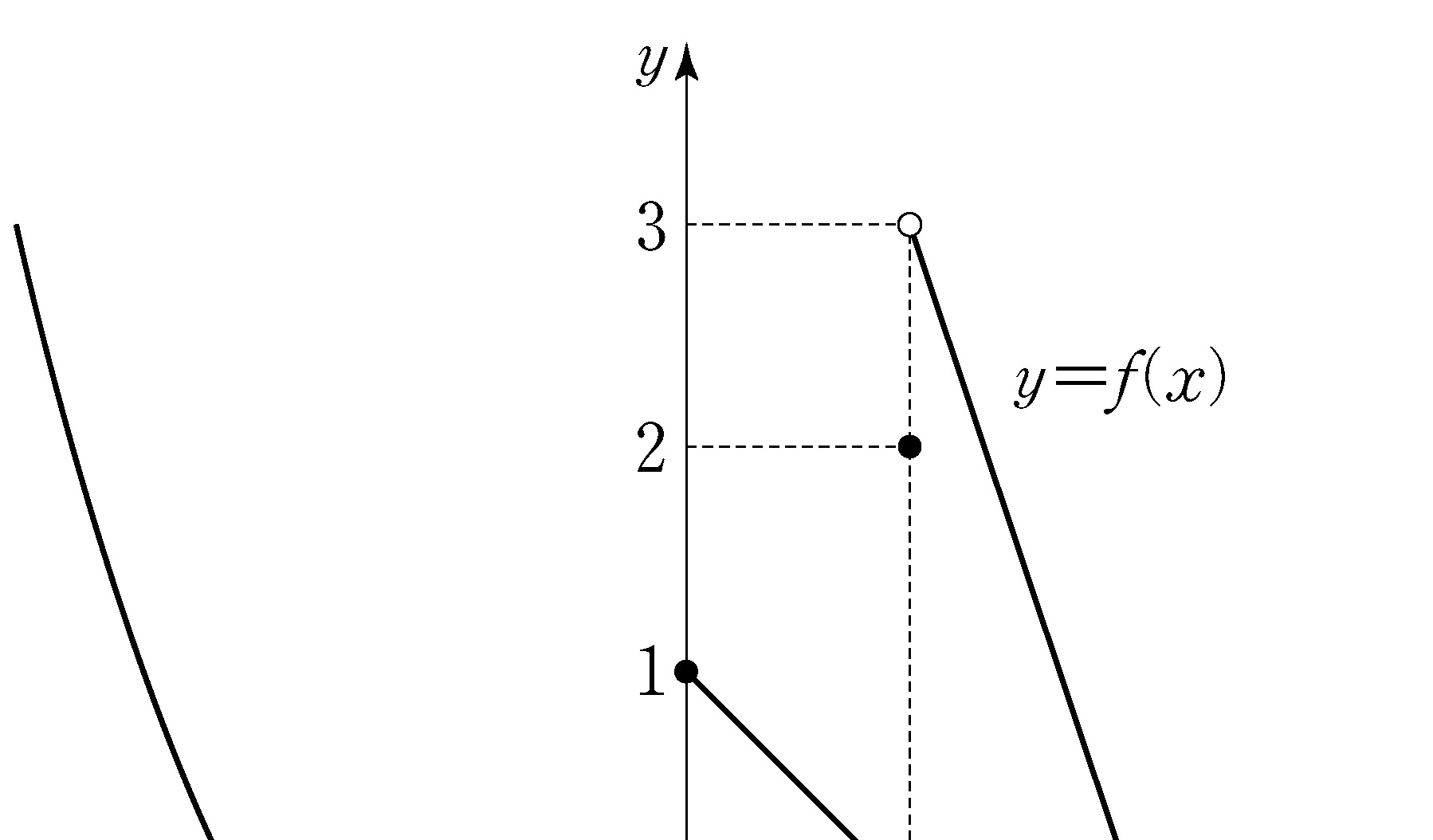
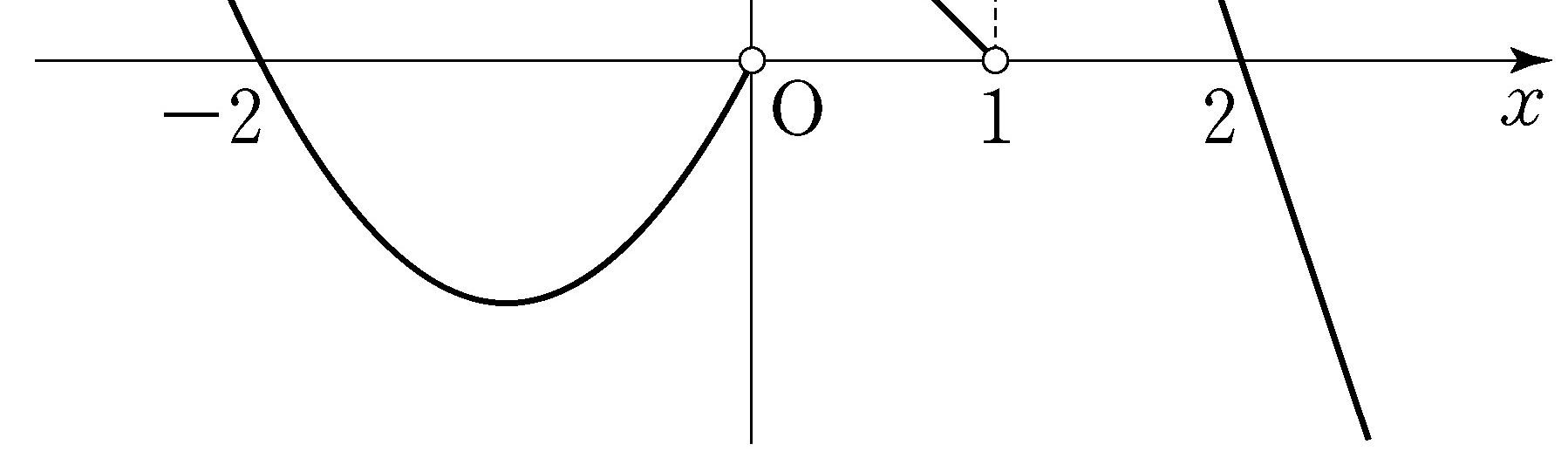
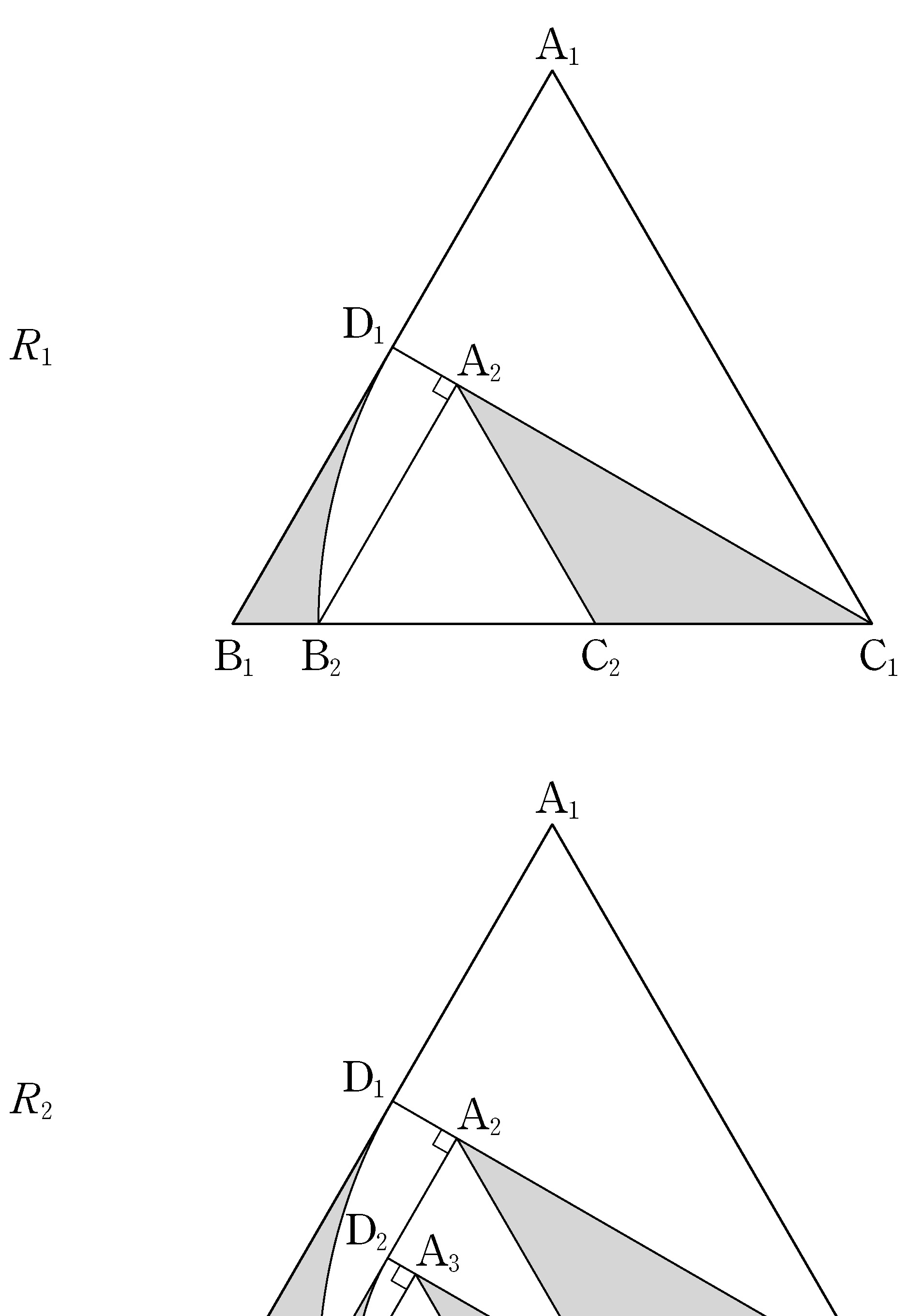
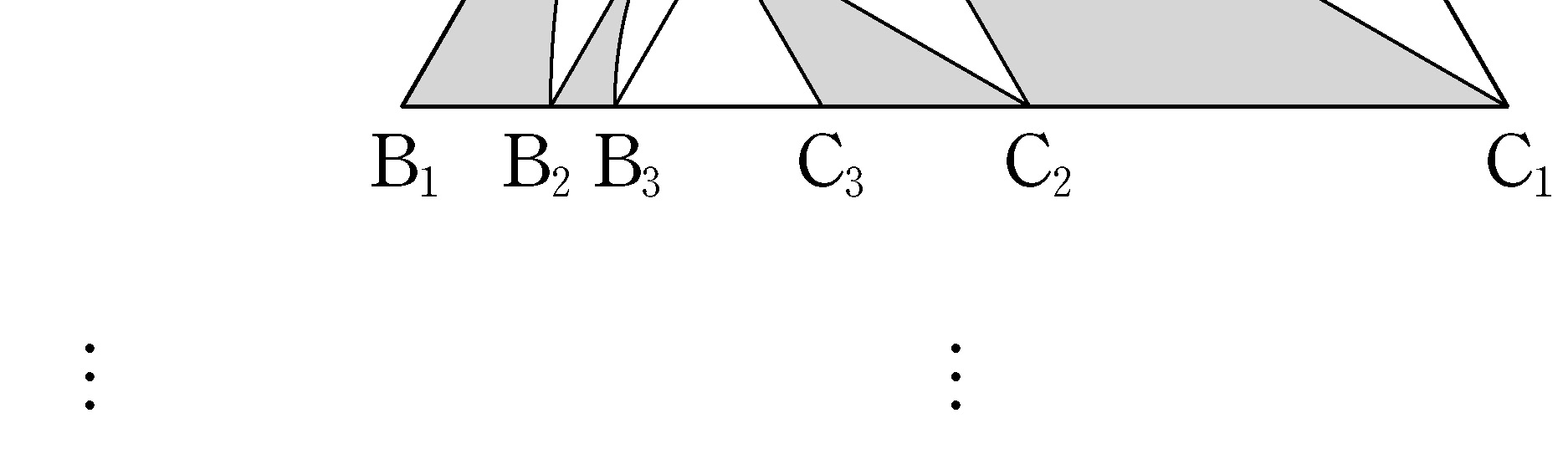
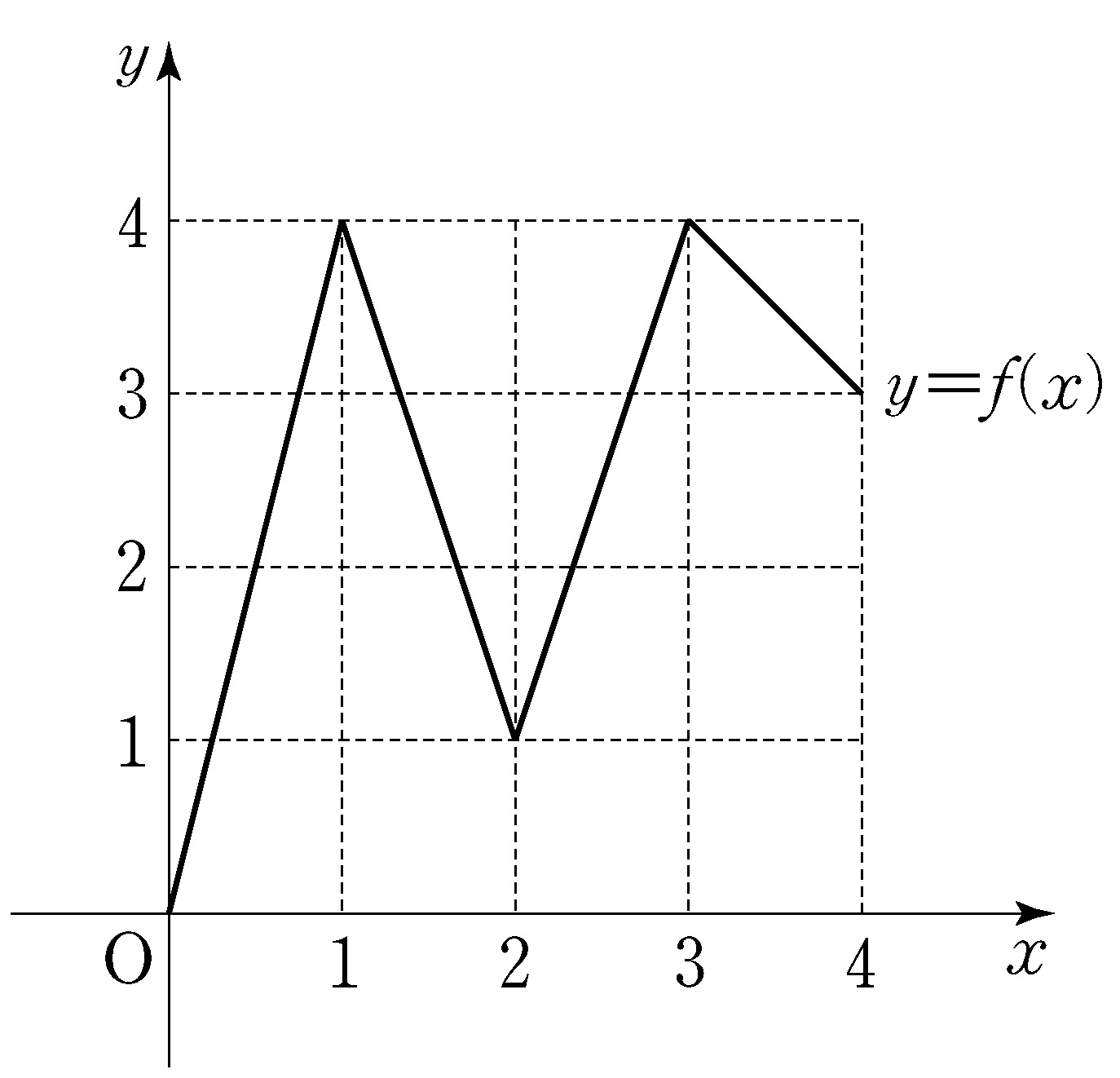
- \(2\)
- \(4\)
- \(6\)
- \(8\)
- \(10\)
2018 College Scholastic Ability Test
Mathematics (Type Na)
Multiple Choice Questions
\(A=\{2,a+1,5\}\:\) and \(\:B=\{2,3,b\}\)
satisfy \(A=B\).
What is the value of \(a+b\)?
(※ \(a\) and \(b\) are real numbers.)
[2 points]
- \(4\)
- \(5\)
- \(6\)
- \(7\)
- \(8\)
- \(\dfrac{1}{5}\)
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{3}\)
- \(\dfrac{1}{2}\)
- \(1\)
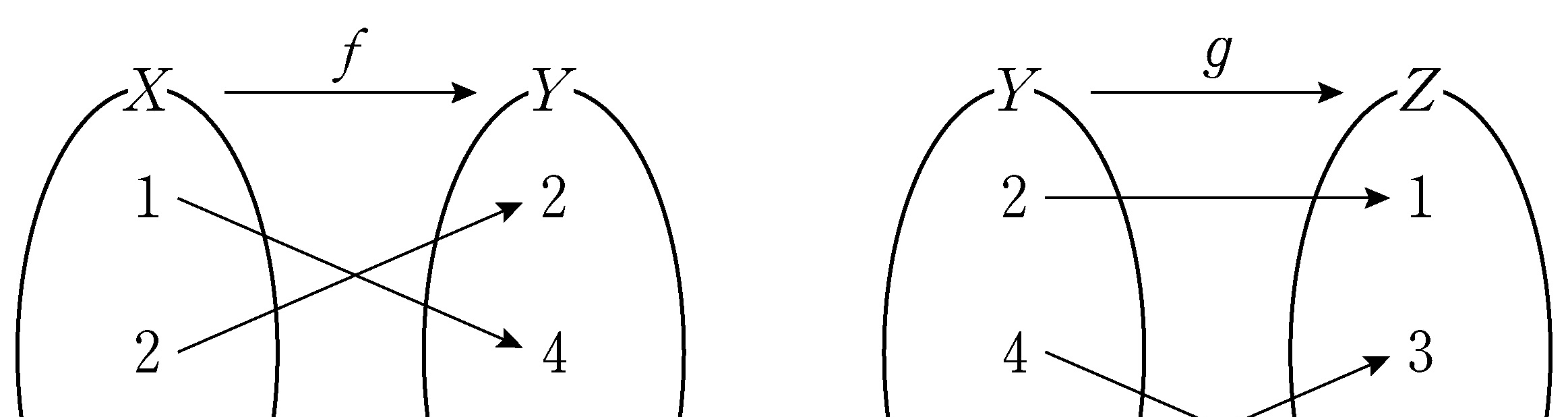

- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)