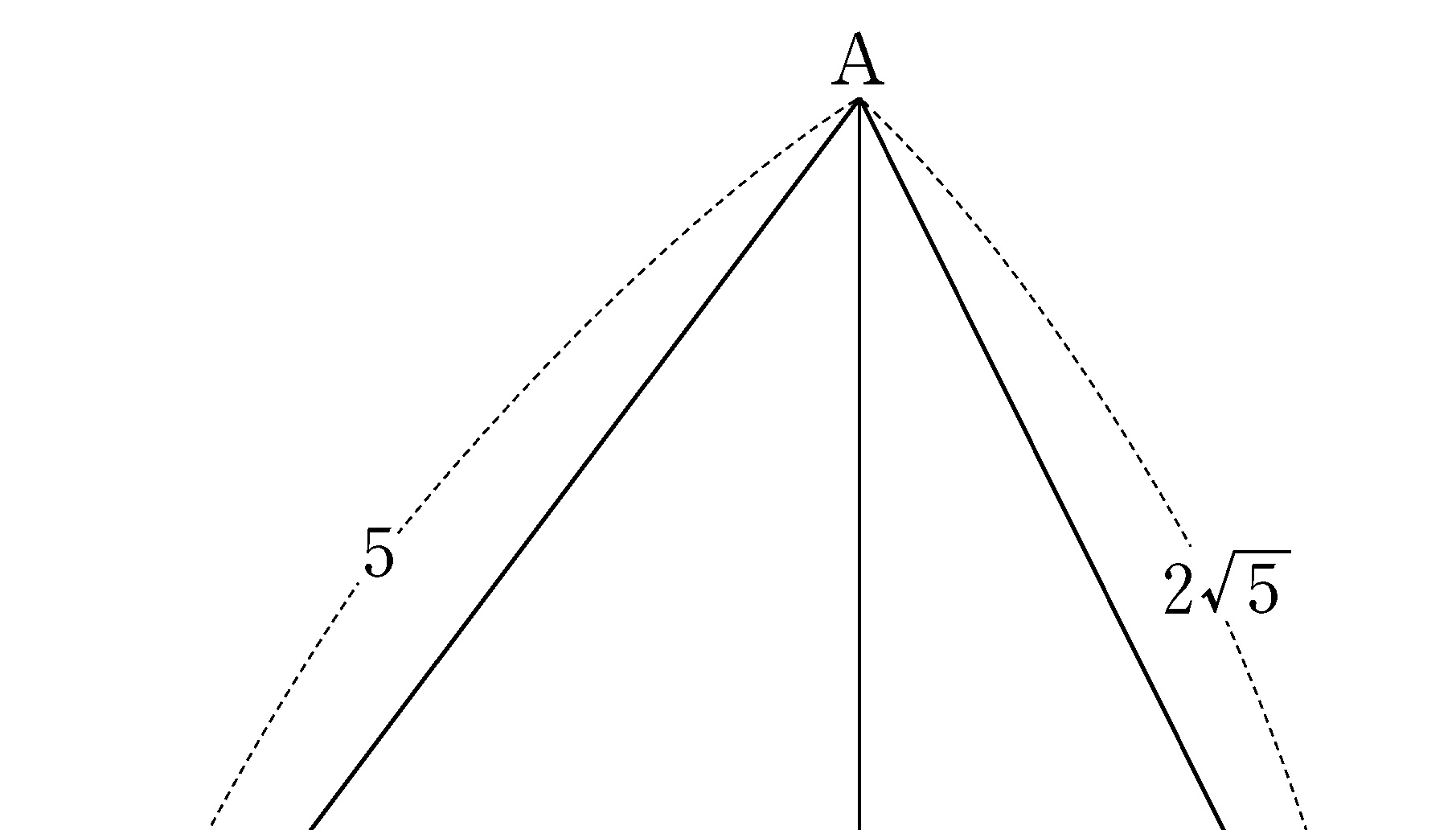
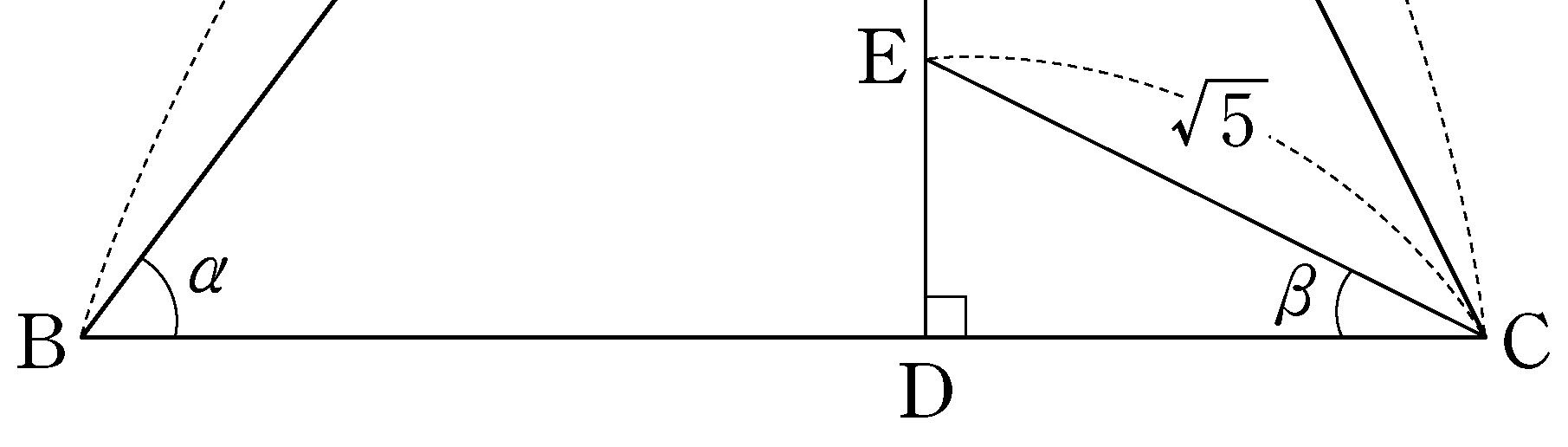
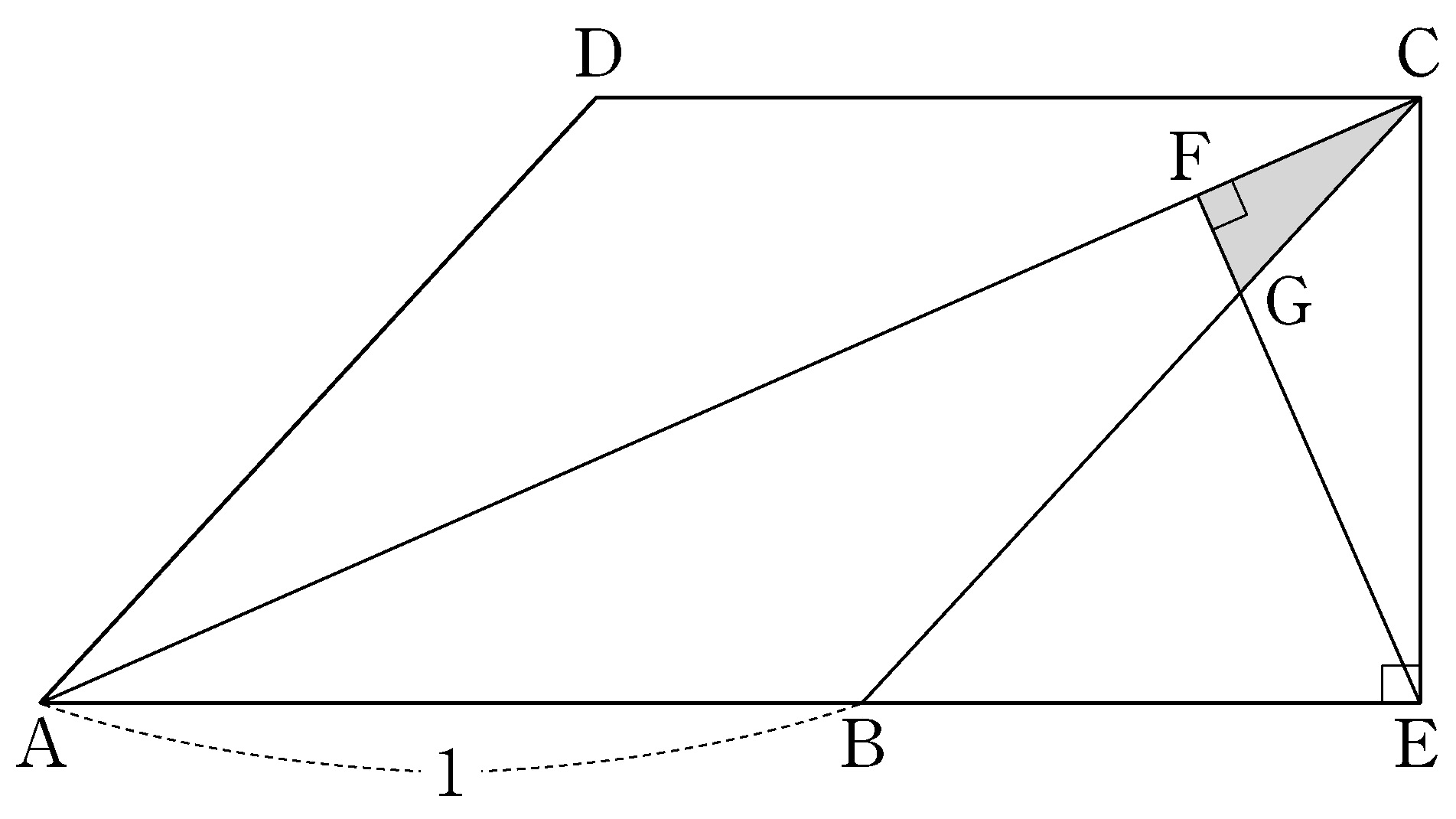
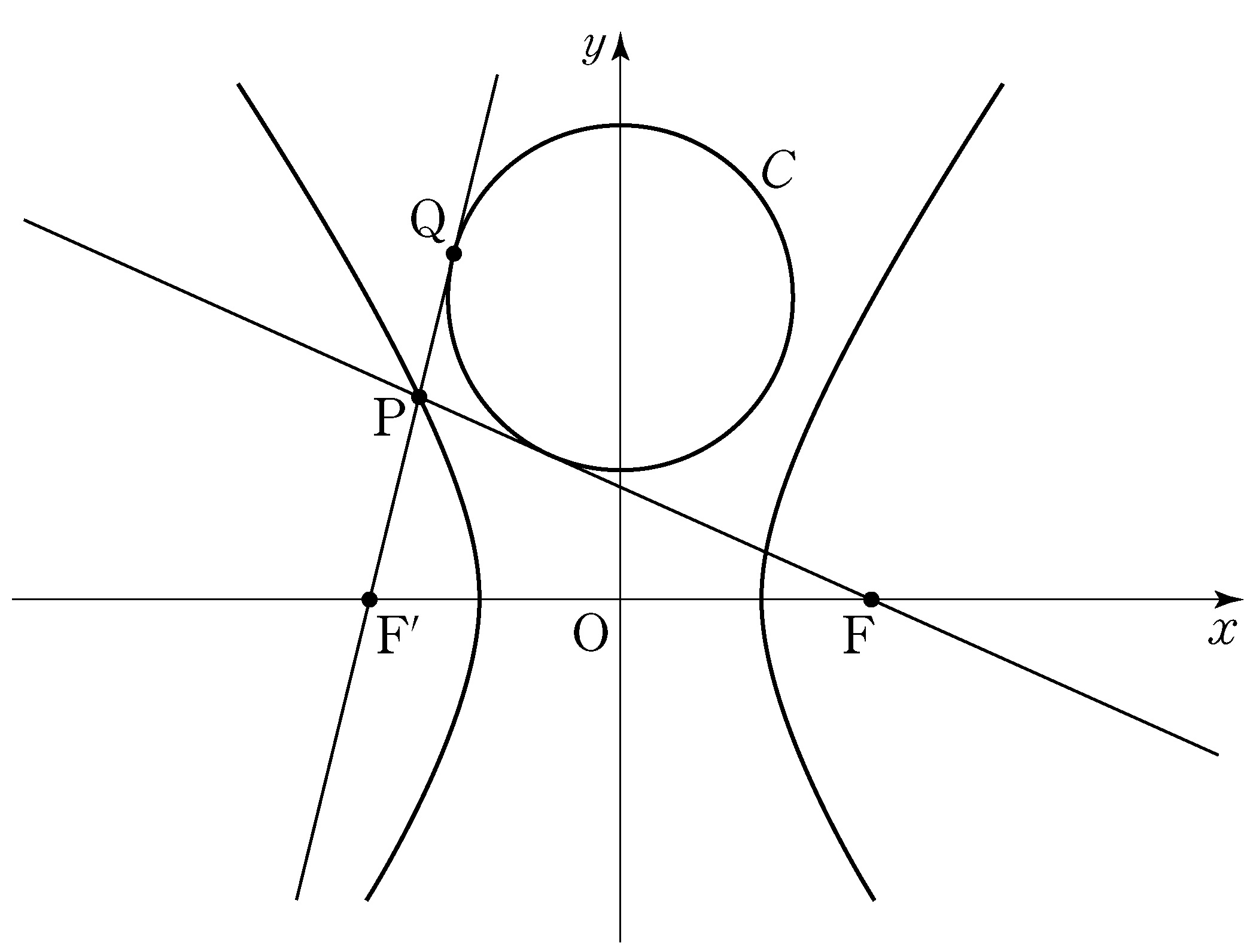
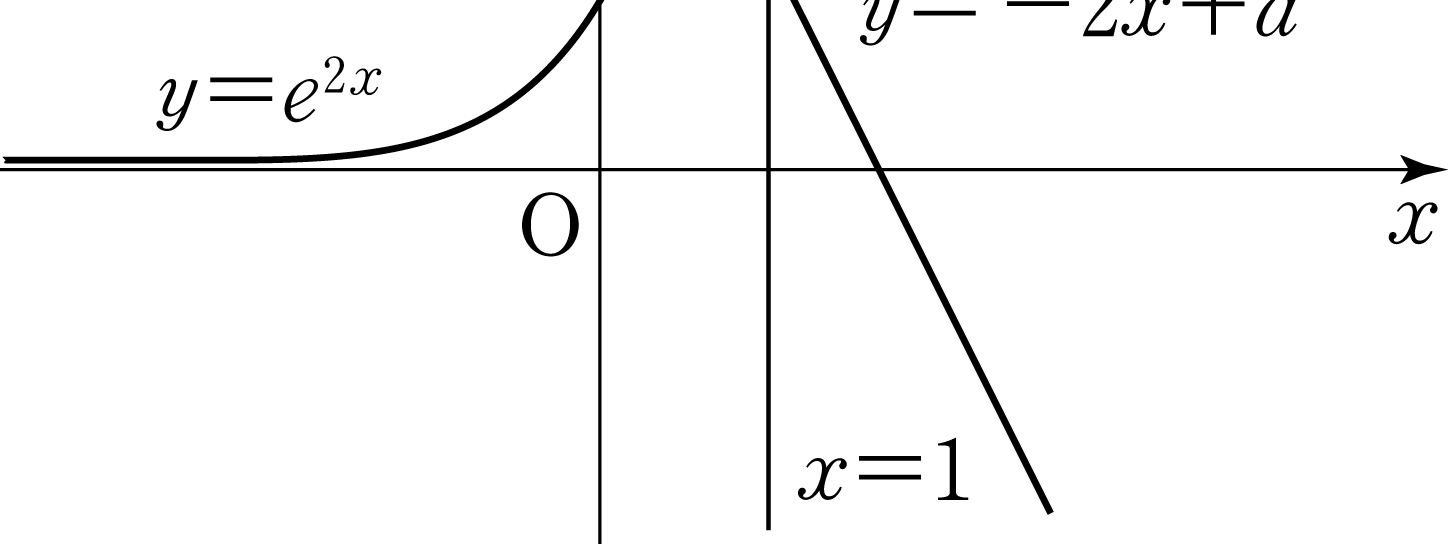- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)
Mathematics (Type Ga)
- \(1\)
- \(\dfrac{4}{3}\)
- \(\dfrac{5}{3}\)
- \(2\)
- \(\dfrac{7}{3}\)
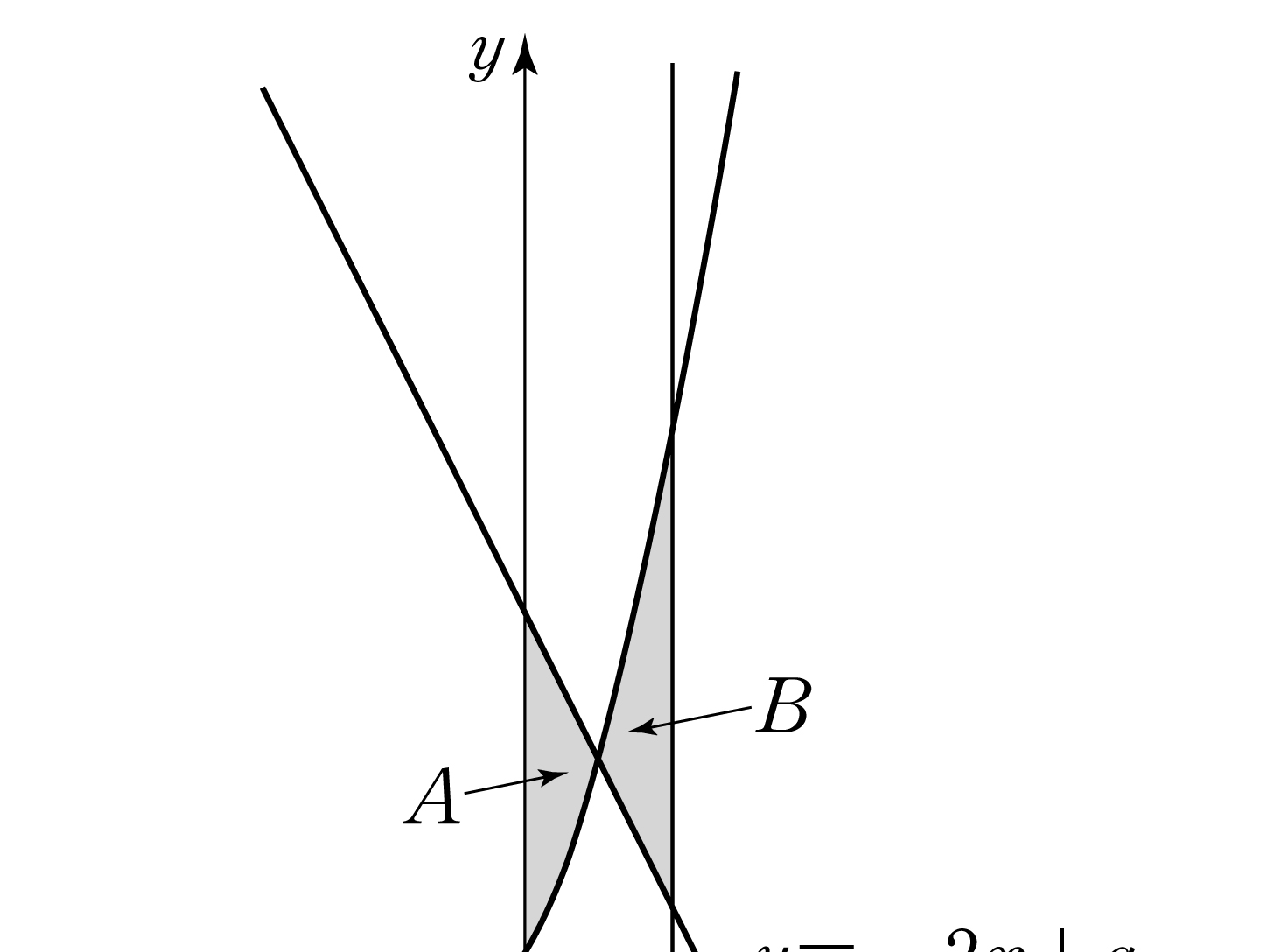
(※ \(1<a<e^2\)) [3 points]
- \(\dfrac{e^2+1}{2}\)
- \(\dfrac{2e^2+1}{4}\)
- \(\dfrac{e^2}{2}\)
- \(\dfrac{2e^2-1}{4}\)
- \(\dfrac{e^2-1}{2}\)
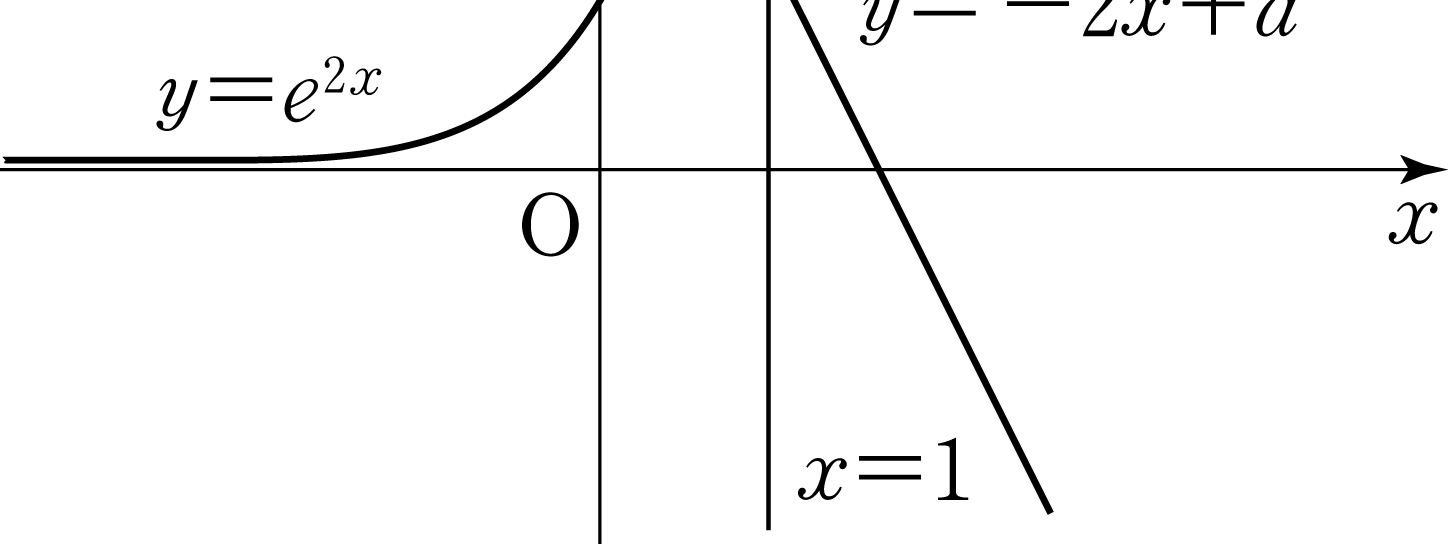
| \(z\) | \(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\) |
| \(1.0\) | \(0.3413\) |
| \(1.5\) | \(0.4332\) |
| \(2.0\) | \(0.4772\) |
| \(2.5\) | \(0.4938\) |