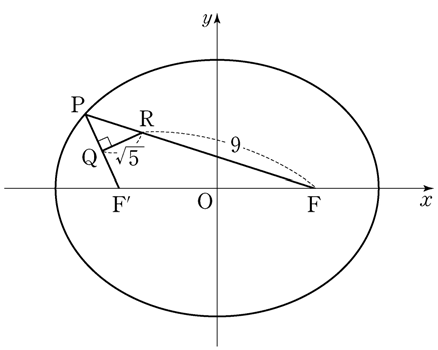
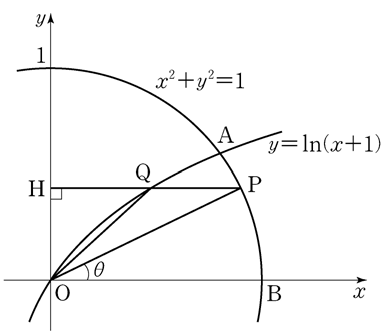
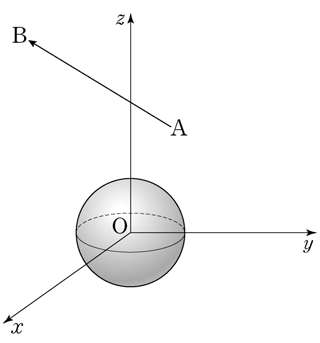
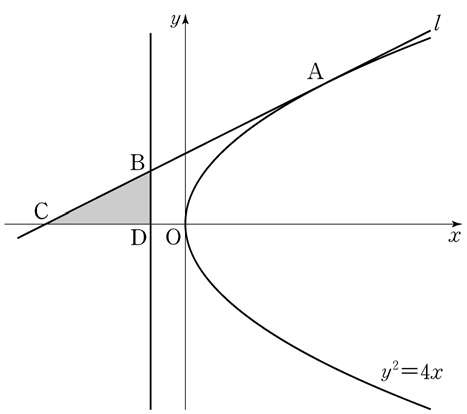
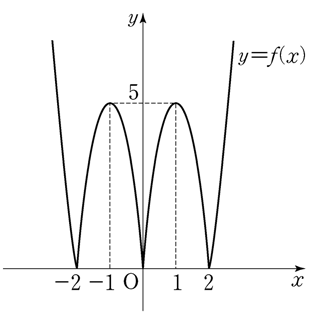
if the sum of all elements in the matrix \(A+B\) is \(9\), what is the value of \(a\)? [2 points]
- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)
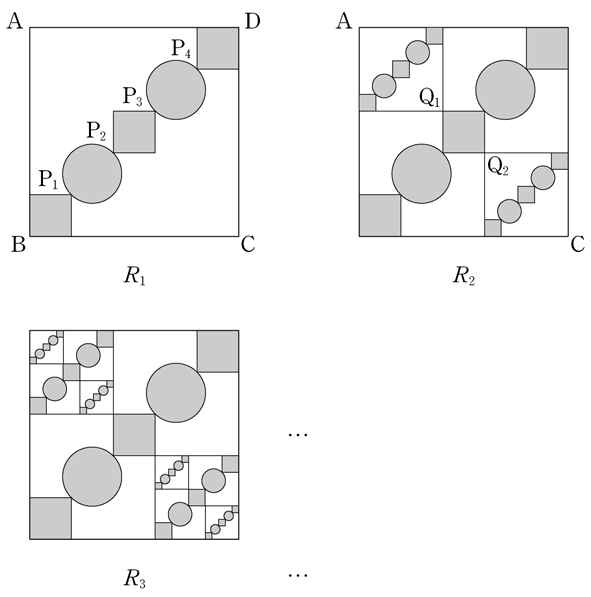
 shape.
shape.
 shapes,
by applying the method used to obtain figure \(R_1\)
to the newly drawn two squares respectively.
shapes,
by applying the method used to obtain figure \(R_1\)
to the newly drawn two squares respectively.
 shapes
on two squares with line segments \(\mathrm{AQ_1}\)
and \(\mathrm{CQ_2}\) as a diagonal respectively,
with the method used to obtain figure \(R_2\) from figure \(R_1\).
shapes
on two squares with line segments \(\mathrm{AQ_1}\)
and \(\mathrm{CQ_2}\) as a diagonal respectively,
with the method used to obtain figure \(R_2\) from figure \(R_1\).
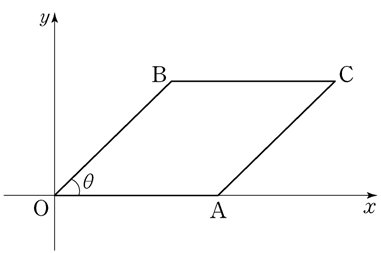
| \(z\) | \(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\) |
| \(1.0\) | \(0.3413\) |
| \(1.2\) | \(0.3849\) |
| \(1.4\) | \(0.4192\) |
| \(1.6\) | \(0.4452\) |