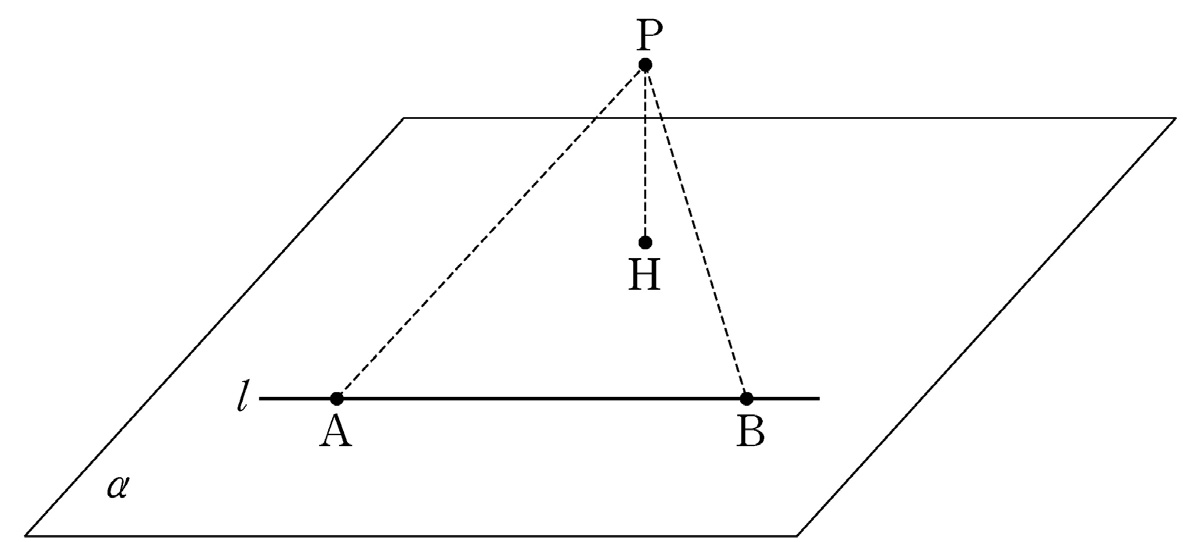
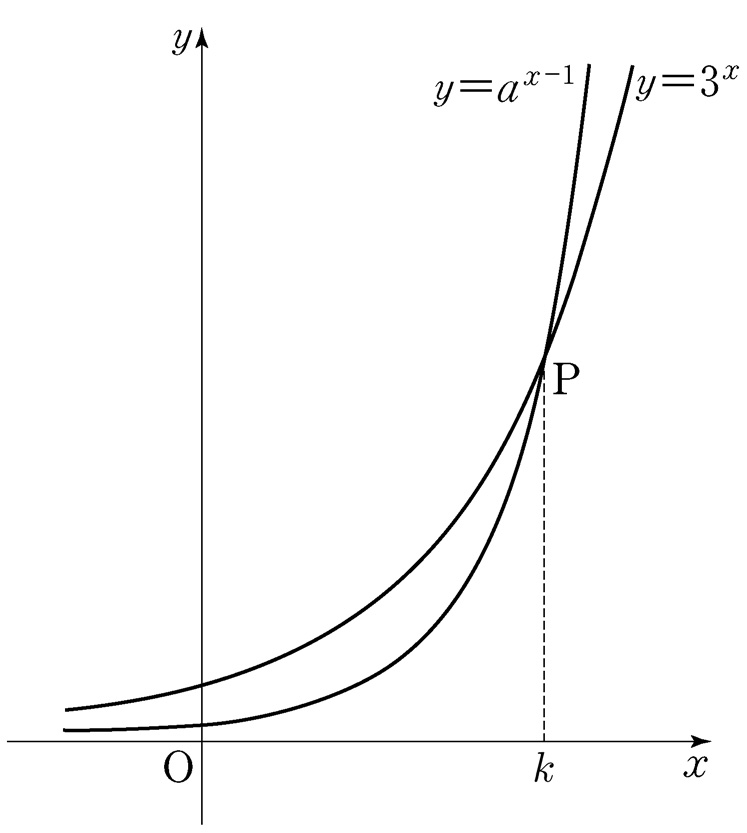
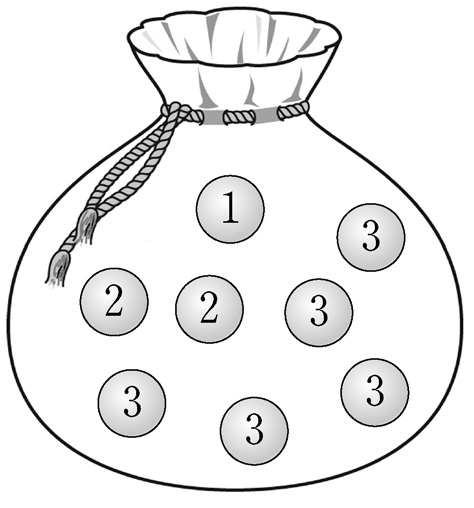
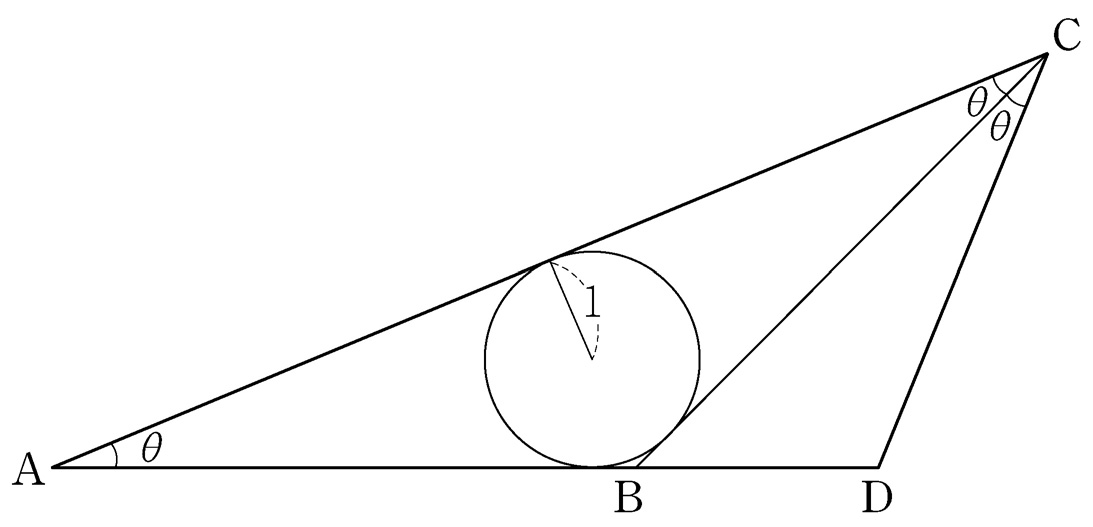
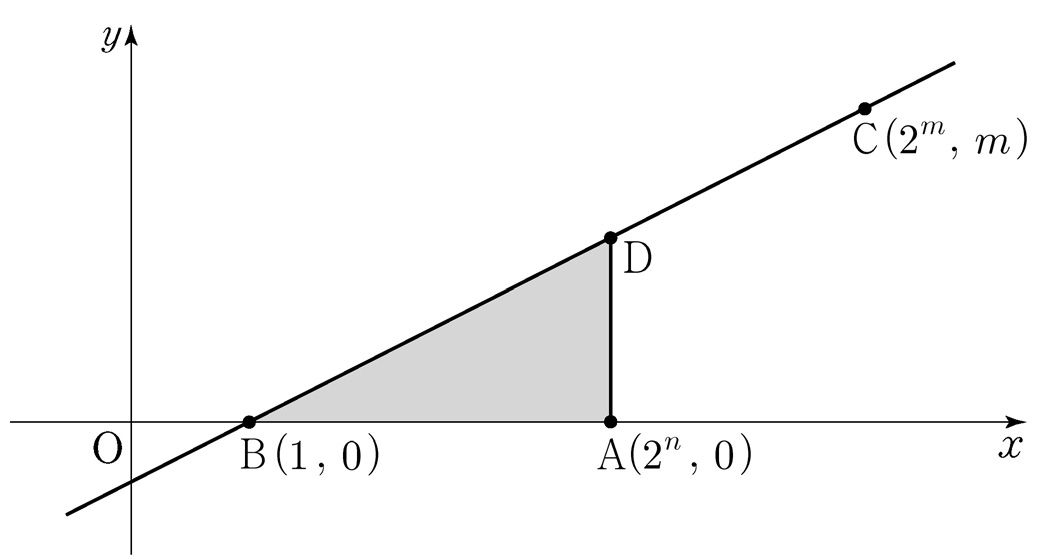
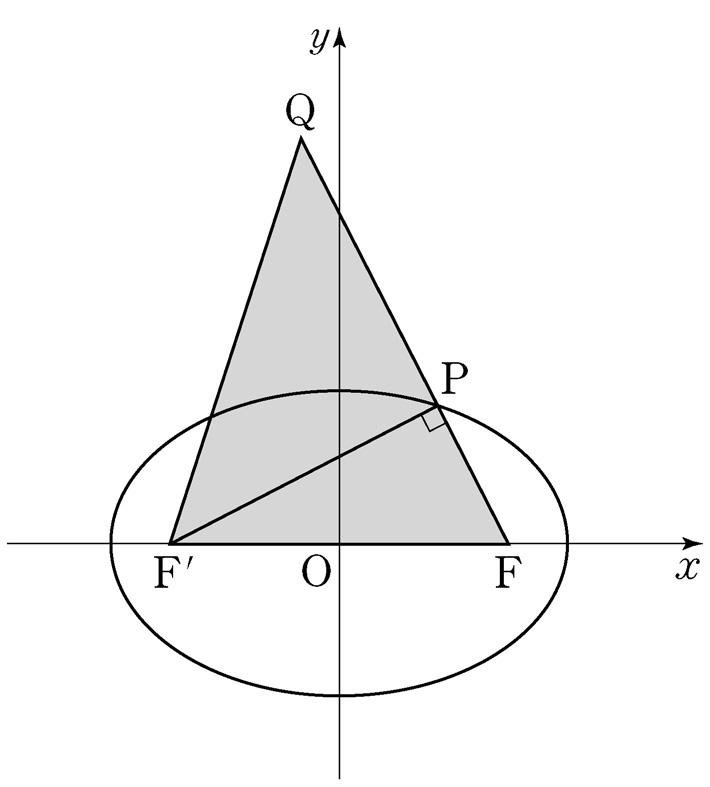
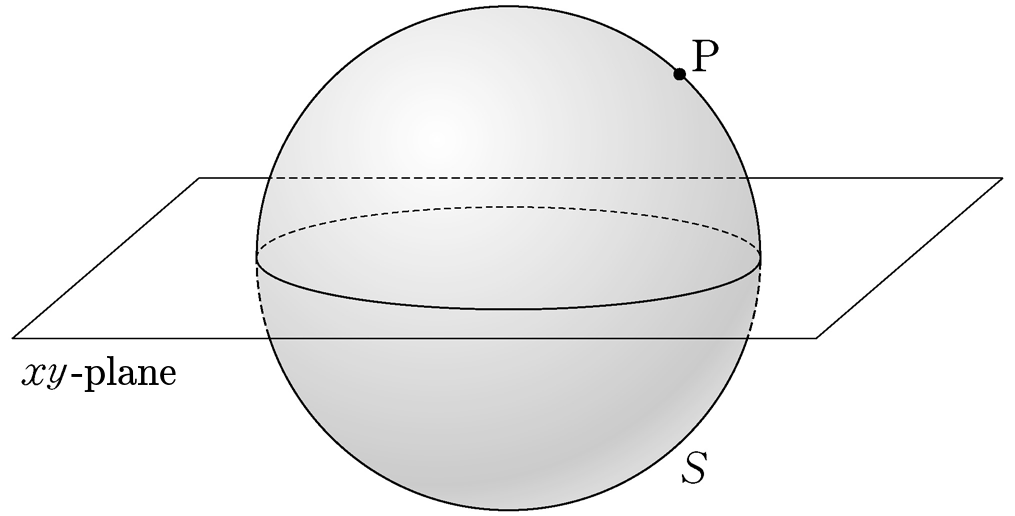
- \(5\)
- \(6\)
- \(7\)
- \(8\)
- \(9\)
Mathematics (Type B)
\(\mathrm{P}(A)=2 \mathrm{P}(B)=\dfrac{3}{5}\),
what is the value of \(\mathrm{P}(A\cap B^C)\)?
(※ \(A^C\) is the complement of \(A\).) [3 points]
- \(\dfrac{7}{20}\)
- \(\dfrac{3}{10}\)
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{5}\)
- \(\dfrac{3}{20}\)
- \(\ln 2\)
- \(\ln 3\)
- \(2\ln 2\)
- \(\ln 5\)
- \(\ln 6\)
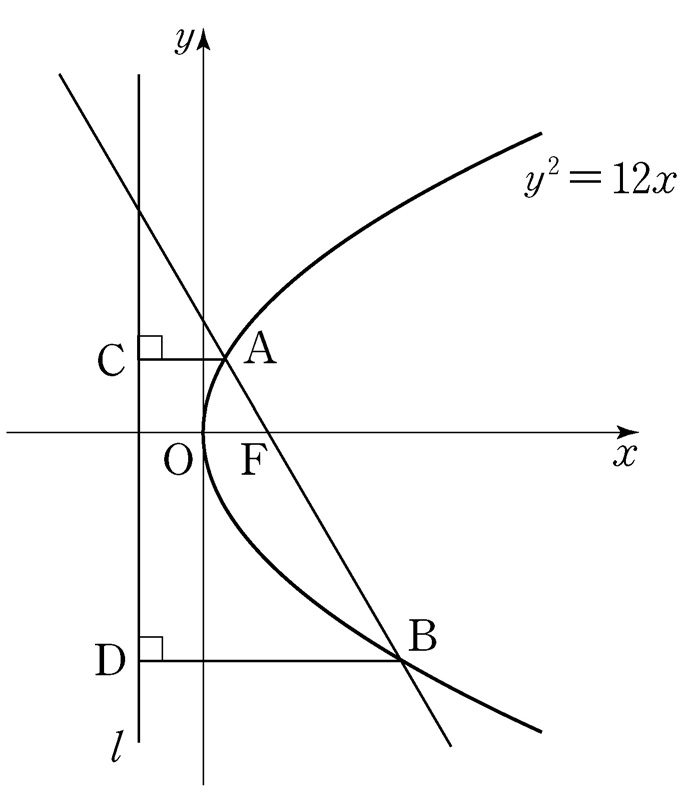
- \(12\)
- \(\dfrac{25}{2}\)
- \(13\)
- \(\dfrac{27}{2}\)
- \(14\)