2014 College Scholastic Ability Test

Mathematics (Type B)

Multiple Choice Questions

For two matrices \(A=\begin{pmatrix} 2&0 \\ 1&0 \end{pmatrix}\) and \(B=\begin{pmatrix} a&0 \\ 2&-3 \end{pmatrix}\),
if the sum of all elements in the matrix \(A+B\) is \(6\), what is the value of \(a\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

If \(\tan\theta= \dfrac{\sqrt{5}}{5}\), what is the value of \(\cos 2\theta\)? [2 points]

\(\dfrac{\sqrt{6}}{3}\)
\(\dfrac{\sqrt{5}}{3}\)
\(\dfrac{2}{3}\)
\(\dfrac{\sqrt{3}}{3}\)
\(\dfrac{\sqrt{2}}{3}\)

For two points \(\mathrm{A}(a, 5, 2)\) and \(\mathrm{B}(-2, 0, 7)\) in
\(3\)-dimensional space, the point internally dividing the line segment \(\mathrm{AB}\) in the ratio \(3:2\) has coordinates \((0,b,5)\). What is the value of \(a+b\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

An arithmetic progression \(\{a_n\}\) with an initial term of \(2\) satisfies \(a_9=3a_3\). What is the value of \(a_5\)? [3 points]

\(10\)
\(11\)
\(12\)
\(13\)
\(14\)

Mathematics (Type B)

Two events \(A\) and \(B\) satisfy

\(\mathrm{P}(A^C\cup B^{\,C})=\dfrac{4}{5}\:\) and \(\:\mathrm{P}(A \cap B^{\,C})=\dfrac{1}{4}\).

What is the value of \(\mathrm{P}(A^C)\)?
(※ \(A^C\) is the complement of \(A\).) [3 points]

\(\dfrac{1}{2}\)
\(\dfrac{11}{20}\)
\(\dfrac{3}{5}\)
\(\dfrac{13}{20}\)
\(\dfrac{7}{10}\)

In \(3\)-dimensional space, a line passing through two points \(\mathrm{A}(5,5,a)\) and \(\mathrm{B}(0,0,3)\) is perpendicular to the line \(x=4-y=z-1\). What is the value of \(a\)? [3 points]

\(3\)
\(5\)
\(7\)
\(9\)
\(11\)

A function \(f(x)=2\cos^2 x+k\sin 2x-1\) has a global maximum value of \(\sqrt{10}\). What is the value of the positive number \(k\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Type B)

On the \(xy\)-plane, two lines \(l_1\) and \(l_2\) which are tangent to the parabola \(y^2=8x\) have slopes of \(m_1\) and \(m_2\) respectively. If \(m_1\) and \(m_2\) are two distinct solutions to the equation \(2x^2-3x+1=0\), what is the \(x\)-coordinate of the intersection of \(l_1\) and \(l_2\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Suppose we select \(5\) numbers among the numbers \(1,2,3\) and \(4\), where each number may be selected multiple times. What is the number of cases where the number \(4\) is selected at most once? [3 points]

\(45\)
\(42\)
\(39\)
\(36\)
\(33\)

As the figure shows, a function \(f(x)\) defined on the closed interval \([-4,4]\) meets the function \(g(x)=- \dfrac{1}{2}x+1\) at three points, whose \(x\)-coordinates are \(\alpha\), \(\beta\) and \(2\) respectively. What is the number of integers \(x\) for which the inequality

\(\dfrac{g(x)}{f(x)}\leq 1\)

is satisfied? (※ \(-4<\alpha<-3\) and \(0<\beta<1\).) [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Type B)

A sequence \(\{a_n\}\) whose terms are all positive, satisfies \(a_1=10\) and

\(\big(a_{n+1}\big)^n=10\big(a_n\big)^{n+1}\quad(n\geq 1)\).

The following is a process computing the general term \(a_n\).

Taking the common logarithm to both sides of the equation gives

\(n\log_{10} a_{n+1}=(n+1)\log_{10}a_n+1\).

Dividing both sides with \(n(n+1)\) gives

\(\dfrac{\log_{10} a_{n+1}}{n+1}=\dfrac{\log_{10}a_n}{n}+ \fbox{\(\;(\alpha)\;\)}\).

Let \(b_n=\dfrac{\log_{10}a_n}{n}\). Then \(b_1=1\) and

\(b_{n+1}=b_n+ \fbox{\(\;(\alpha)\;\)}\).

The general term of the sequence \(\{b_n\}\) is

\(b_n= \fbox{\(\;(\beta)\;\)}\),

therefore

\(\log_{10}a_n=n\times \fbox{\(\;(\beta)\;\)}\).

Therefore \(a_n=10^{n\times \fbox{\(\;(\beta)\;\)}}\).

Let \(f(n)\) and \(g(n)\) be the correct expression for \(\alpha\) and \(\beta\) respectively. What is the value of \(\dfrac{g(10)}{f(4)}\)? [3 points]

\(38\)
\(40\)
\(42\)
\(44\)
\(46\)

For a quadratic function \(f(x)\) whose term with degree two has a coefficient of \(1\), and the function

\(g(x)= \begin{cases} \dfrac{1}{\ln(x+1)} &\; (x \ne 0) \\\\ \qquad 8 &\; (x=0), \end{cases}\)

the function \(f(x)g(x)\) is continuous on the interval \((-1,\infty)\). What is the value of \(f(3)\)? [3 points]

\(6\)
\(9\)
\(12\)
\(15\)
\(18\)

Mathematics (Type B)

[13~14] As the figure shows, there is a line \(\boldsymbol{l:x-y-1=0}\) and a hyperbola \(\boldsymbol{C:x^2-2y^2=1}\) with a point \(\boldsymbol{\mathrm{F}(c,0)}\) (※ \(\boldsymbol{c<0}\)) as one of its foci. Answer the questions 13 and 14.

What is the volume of the solid formed by rotating the region enclosed by line \(l\) and hyperbola \(C\) about the \(y\)-axis? [3 points]

\(\dfrac{5}{3}\pi\)
\(\dfrac{3}{2}\pi\)
\(\dfrac{4}{3}\pi\)
\(\dfrac{7}{6}\pi\)
\(\pi\)

A linear map that performs a rotation of \(\theta\) about the origin, maps the line \(l\) to a line that passes a focus \(\mathrm{F}\) of the hyperbola \(C\). What is the value of \(\sin 2\theta\)? [4 points]

\(-\dfrac{2}{3}\)
\(-\dfrac{5}{9}\)
\(-\dfrac{4}{9}\)
\(-\dfrac{1}{3}\)
\(-\dfrac{2}{9}\)

Mathematics (Type B)

Consider a rectangle \(\mathrm{A_1B_1C_1D_1}\) with \(\overline{\mathrm{A_1B_1}}=1\) and \(\overline{\mathrm{A_1D_1}}=2\). As the figure shows, let \(\mathrm{M_1}\) and \(\mathrm{N_1}\) be the midpoints of line segments \(\mathrm{A_1D_1}\) and \(\mathrm{B_1C_1}\) respectively. Let us draw a sector \(\mathrm{N_1M_1B_1}\) with center \(\mathrm{N_1}\), radius \(\overline{\mathrm{B_1N_1}}\), and centeral angle \(\dfrac{\pi}{2}\). Let us draw a sector \(\mathrm{D_1M_1C_1}\) with center \(\mathrm{D_1}\), radius \(\overline{\mathrm{C_1D_1}}\), and centeral angle \(\dfrac{\pi}{2}\). Figure \(R_1\) is obtained by coloring the

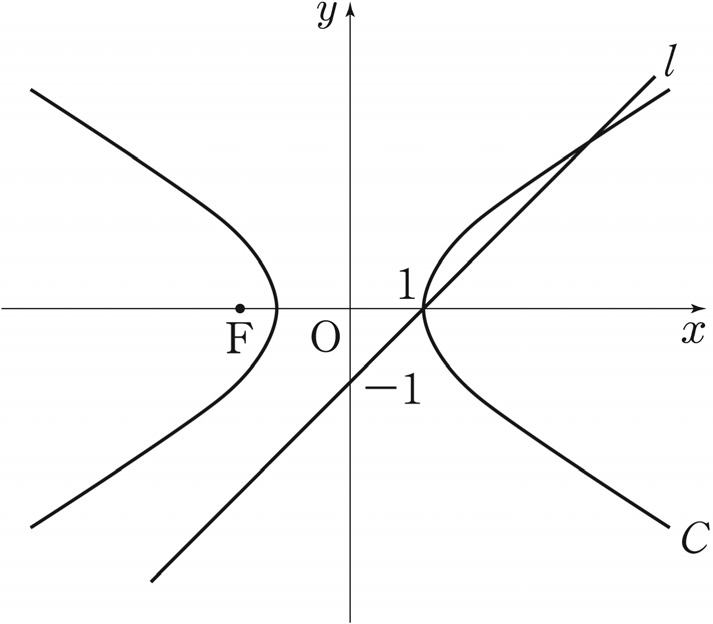
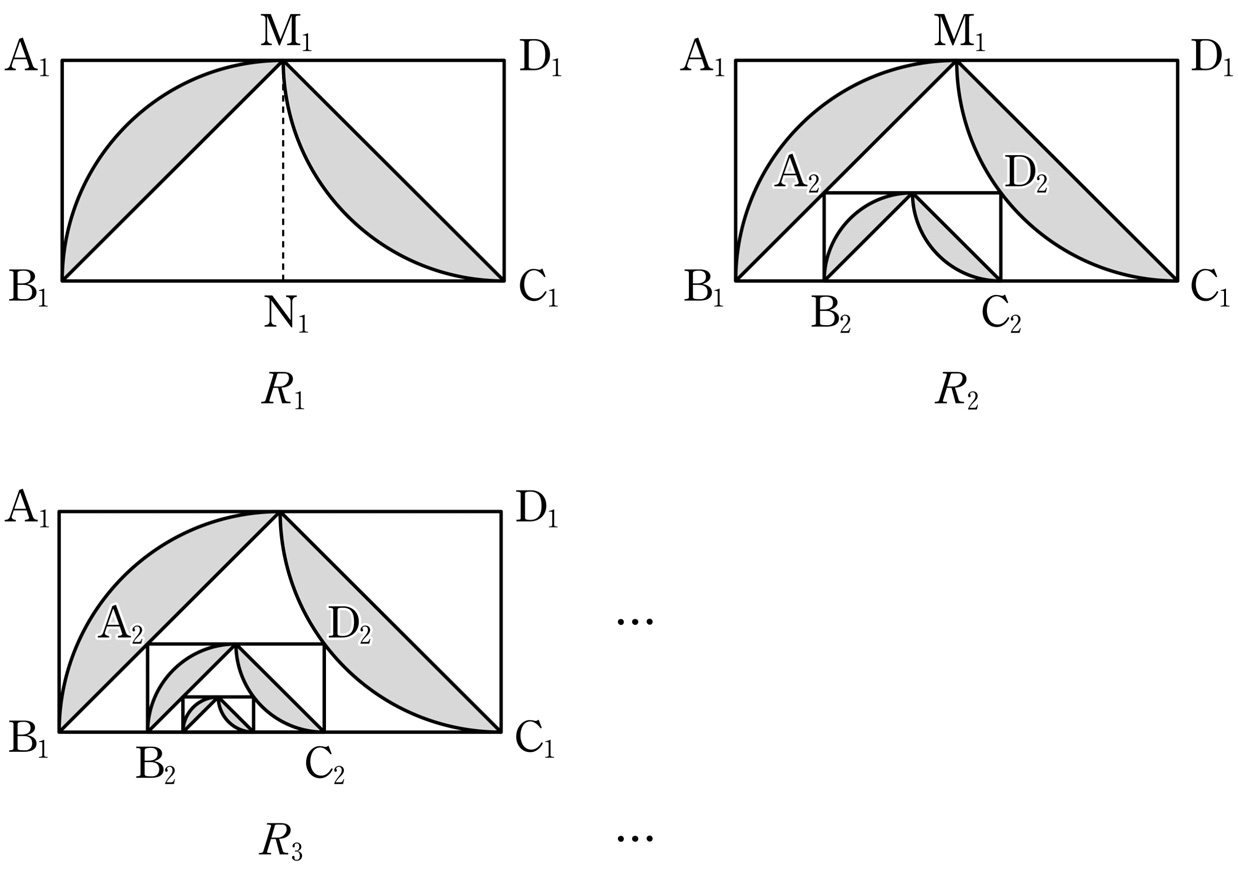
shape consisting of the region enclosed by arc \(\mathrm{M_1B_1}\) of sector \(\mathrm{N_1M_1B_1}\) and line \(\mathrm{M_1B_1}\), and the region enclosed by arc \(\mathrm{M_1C_1}\) of sector \(\mathrm{D_1M_1C_1}\) and line \(\mathrm{M_1C_1}\).
Starting from figure \(R_1\), let us draw a rectangle \(\mathrm{A_2B_2C_2D_2}\) where \(\mathrm{A_2}\) is on line \(\mathrm{M_1B_1}\), \(\mathrm{D_2}\) is on arc \(\mathrm{M_1C_1}\), \(\mathrm{B_2}\) and \(\mathrm{C_2}\) are on the edge \(\mathrm{B_1C_1}\), and \(\overline{\mathrm{A_2B_2}}:\overline{\mathrm{A_2D_2}}=1:2\). With the same method used to obtain figure \(R_1\), figure \(R_2\) is obtained by drawing and coloring the

shape inside rectangle \(\mathrm{A_2B_2C_2D_2}\).
Continue this process, and let \(S_n\) be the area of the colored region in \(R_n\), the \(n\)th obtained figure.
What is the value of \(\displaystyle\lim_{n\to\infty} S_n\)? [4 points]

\(\dfrac{25}{19}\!\left(\!\dfrac{\pi}{2}-1\!\right)\)
\(\dfrac{5}{4}\!\left(\!\dfrac{\pi}{2}-1\!\right)\)
\(\dfrac{25}{21}\!\left(\!\dfrac{\pi}{2}-1\!\right)\)
\(\dfrac{25}{22}\!\left(\!\dfrac{\pi}{2}-1\!\right)\)
\(\dfrac{25}{23}\!\left(\!\dfrac{\pi}{2}-1\!\right)\)

A random variable \(X\) defined on the closed interval \([0,a]\) has a continuous probability density function. If the random variable \(X\) satisfies the following, what is the value of the constant \(k\)? [4 points]

\(\mathrm{P}(0\leq X\leq x)=kx^2\) for all \(x\) in \(0\leq x\leq a\).
\(\mathrm{E}(X)=1\)

\(\dfrac{9}{16}\)
\(\dfrac{4}{9}\)
\(\dfrac{1}{4}\)
\(\dfrac{1}{9}\)
\(\dfrac{1}{16}\)

Mathematics (Type B)

Two square matrices \(A\) and \(B\) of order \(2\) satisfy

\(AB+A^2B=E\:\) and \(\:(A-E)^2+B^2=O\).

Which option only contains every correct statement in the <List>? (※ \(E\) is the identity matrix and \(O\) is the zero matrix.) [4 points]

\(B\) is invertible.
\(AB=BA\)
\((A^3-A)^2+E=O\)

b
c
a, b
a, c
a, b, c

For a positive integer \(n\), let \(a_n\) be the \(n\)th smallest number in the list of all \(x\)-coordinates of points in the \(1\)st quadrant, where the line \(y=n\) meets the graph of the function \(y=\tan x\).
What is the value of \(\displaystyle\lim_{n\to\,\infty}\dfrac{a_n}{n}\)? [4 points]

\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{2}\)
\(\dfrac{3}{4}\pi\)
\(\pi\)
\(\dfrac{5}{4}\pi\)

Mathematics (Type B)

In \(3\)-dimensional space, consider a sphere \(S\) whose center has positive \(x\), \(y\), and \(z\)-coordinates. The sphere \(S\) is tangent to the \(x\)-axis and the \(y\)-axis, and meets the \(z\)-axis at two distinct points. The intersection of sphere \(S\) and the \(xy\)-plane is a circle with an area of \(64\pi\), and the distance between the two intersections of sphere \(S\) and the \(z\)-axis is \(8\). What is the radius of sphere \(S\)? [4 points]

\(11\)
\(12\)
\(13\)
\(14\)
\(15\)

For a real number \(x\) greater than \(1\), let \(f(x)\) and \(g(x)\) be the characteristic and mantissa of \(\log_{10}x\) respectively. Let us list all values of \(x\) for which \(3f(x)+5g(x)\) is a multiple of \(10\). Let \(a\) be the \(2\)nd smallest number in this list, and \(b\) be the \(6\)th smallest number in this list. What is the value of \(\log_{10} ab\)? [4 points]

\(8\)
\(10\)
\(12\)
\(14\)
\(16\)

Mathematics (Type B)

The graph of a continuous function \(y=f(x)\) is symmetric about the origin, and

\(f(x)=\dfrac{\pi}{2}\displaystyle\int_{1}^{x+1}\!f(t)dt\)

for all real numbers \(x\). What is the value of

\(\pi^2 \displaystyle\int_{0}^{1}xf(x+1)dx\),

given that \(f(1)=1\)? [4 points]

\(2(\pi-2)\)
\(2\pi-3\)
\(2(\pi-1)\)
\(2\pi-1\)
\(2\pi\)

Short Answer Questions

For the function \(f(x)=5e^{3x-3}\), compute \(f'(1)\). [3 points]

Among \(50\) members of a marathon club who participated in some marathon race, the number of members who finished or retired is as follows.

(Unit: people)

	Male	Female
Finished	\(27\)	\(9\)
Retired	\(8\)	\(6\)

Suppose a member who participated in this race was chosen at random. Given that this member is female, the probability that this member finished the marathon is \(p\). Compute \(100p\). [3 points]

Mathematics (Type B)

Let \(k\) be the product of all real solutions to the equation \(\sqrt{2x^2-6x}=x^2-3x-4\). Compute \(k^2\). [3 points]

Suppose water completely fills and flows in a cylindrical pipe, whose cross section has a radius of \(R\,(R<1)\). Let \(v_c\) be the speed of water at the center of a cross section of this pipe, and let \(v\) be the speed of water at a point \(x\,(0<x \leq R)\) units apart from the walls of the pipe towards the center. Then the following relation is known.

\(\dfrac{v_c}{v}=1-k\log_{10} \dfrac{x}{R}\)

(※ \(k\) is a positive constant. Then units of length and speed are \(\text{m}\) and \(\text{m/s}\) respectively.)

For this pipe satisfying \(R< 1\), the speed of water at a point \(R^{\small{\dfrac{27}{23}}}\) units apart from the walls towards the center is \(\dfrac{1}{2}\) times the speed of water at the center, and the speed of water at a point \(R^a\) units apart from the walls towards the center is \(\dfrac{1}{3}\) times the speed of water at the center. Compute \(23a\). [3 points]

Suppose we took a random sample of \(n\) people from the residents of some city to find the proportion of people who have used the central park of the city, and \(80\%\) of people answered that they have used it. Using this result, a \(95\%\) confidence interval for the proportion of all residents of this city who have used the central park, is computed to be \([a,b]\). Given that \(b-a=0.098\), compute \(n\).
(※ For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(|Z| \leq 1.96) = 0.95\).) [4 points]

Mathematics (Type B)

As the figure shows, there is a point \(\mathrm{A}(0,a)\) on the \(y\)-axis, and a point \(\mathrm{P}\) that moves on the ellipse \(\dfrac{x^2}{25}+ \dfrac{y^2}{9}=1\) with two foci \(\mathrm{F}\) and \(\mathrm{F'}\). Given that the minimum value of \(\overline{\mathrm{AP}}- \overline{\mathrm{FP}}\) is \(1\), compute \(a^2\). [4 points]

As the figure shows, there is an isosceles triangle \(\mathrm{ABC}\) where the line segment \(\mathrm{AB}\) has a length of \(4\), \(\overline{\mathrm{AC}} = \overline{\mathrm{BC}}\), and \(\angle \mathrm{ACB}=\theta\). Let \(\mathrm{D}\) be a point on the extended line \(\mathrm{AB}\) such that \(\overline{\mathrm{AC}} = \overline{\mathrm{AD}}\), and let \(\mathrm{P}\) be a point such that \(\overline{\mathrm{AC}} = \overline{\mathrm{AP}}\) and \(\angle \mathrm{PAB}=2\theta\).
Let \(S(\theta)\) be the area of the triangle \(\mathrm{BDP}\).
Compute \(\displaystyle\lim_{\theta\to\,+0}(\theta\times S(\theta))\). (※ \(0< \theta< \dfrac{\pi}{6}\)) [4 points]

Mathematics (Type B)

In \(3\)-dimensional space, suppose two points \(\mathrm{P}\) and \(\mathrm{Q}\) are moving on the sphere \(x^2+y^2+z^2=4\). Let \(\mathrm{P_1}\) and \(\mathrm{Q_1}\) be perpendicular foots from points \(\mathrm{P}\) and \(\mathrm{Q}\) to the plane \(y=4\) respectively, and let \(\mathrm{P_2}\) and \(\mathrm{Q_2}\) be perpendicular foots from points \(\mathrm{P}\) and \(\mathrm{Q}\) to the plane \(y+\sqrt{3}z+8=0\) respectively. Compute the maximum value of \(2\big|\overrightarrow{\mathrm{PQ}}\big|^2 -\big|\overrightarrow{\mathrm{P_1Q_1}}\big|^2 -\big|\overrightarrow{\mathrm{P_2Q_2}}\big|^2\). [4 points]

For a quadratic function \(f(x)\), the function \(g(x)=f(x)e^{-x}\) satisfies the following.

Points \((1,g(1))\) and \((4,g(4))\) are inflection points of the curve \(y=g(x)\).
The number of tangent lines to the curve \(y=g(x)\) that passes through point \((0,k)\) is \(3\) if and only if \(-1<k<0\).

Compute \(g(-2)\times g(4)\). [4 points]