- \(12\)
- \(10\)
- \(8\)
- \(6\)
- \(4\)
2014 College Scholastic Ability Test
Mathematics (Type A)
Multiple Choice Questions
- \(8\)
- \(9\)
- \(10\)
- \(11\)
- \(12\)
- \(10\)
- \(9\)
- \(8\)
- \(7\)
- \(6\)
- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)

| \(z\) | \(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\) |
| \(1.5\) | \(0.4332\) |
| \(2.0\) | \(0.4772\) |
| \(2.5\) | \(0.4938\) |
| \(3.0\) | \(0.4987\) |
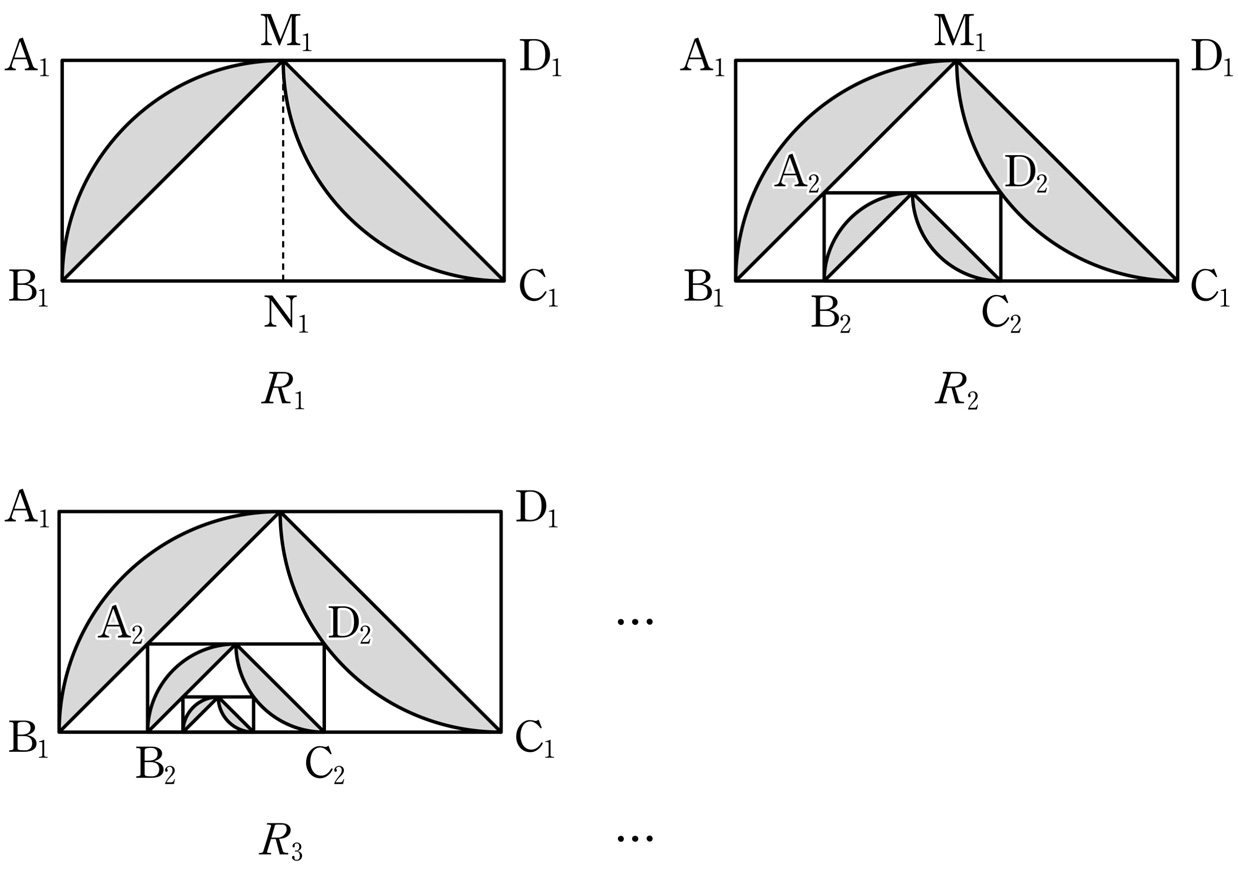
 shape
consisting of the region enclosed by
arc \(\mathrm{M_1B_1}\) of sector \(\mathrm{N_1M_1B_1}\) and line \(\mathrm{M_1B_1}\),
and the region enclosed by
arc \(\mathrm{M_1C_1}\) of sector \(\mathrm{D_1M_1C_1}\) and line \(\mathrm{M_1C_1}\).
shape
consisting of the region enclosed by
arc \(\mathrm{M_1B_1}\) of sector \(\mathrm{N_1M_1B_1}\) and line \(\mathrm{M_1B_1}\),
and the region enclosed by
arc \(\mathrm{M_1C_1}\) of sector \(\mathrm{D_1M_1C_1}\) and line \(\mathrm{M_1C_1}\).
 shape
inside rectangle \(\mathrm{A_2B_2C_2D_2}\).
shape
inside rectangle \(\mathrm{A_2B_2C_2D_2}\).