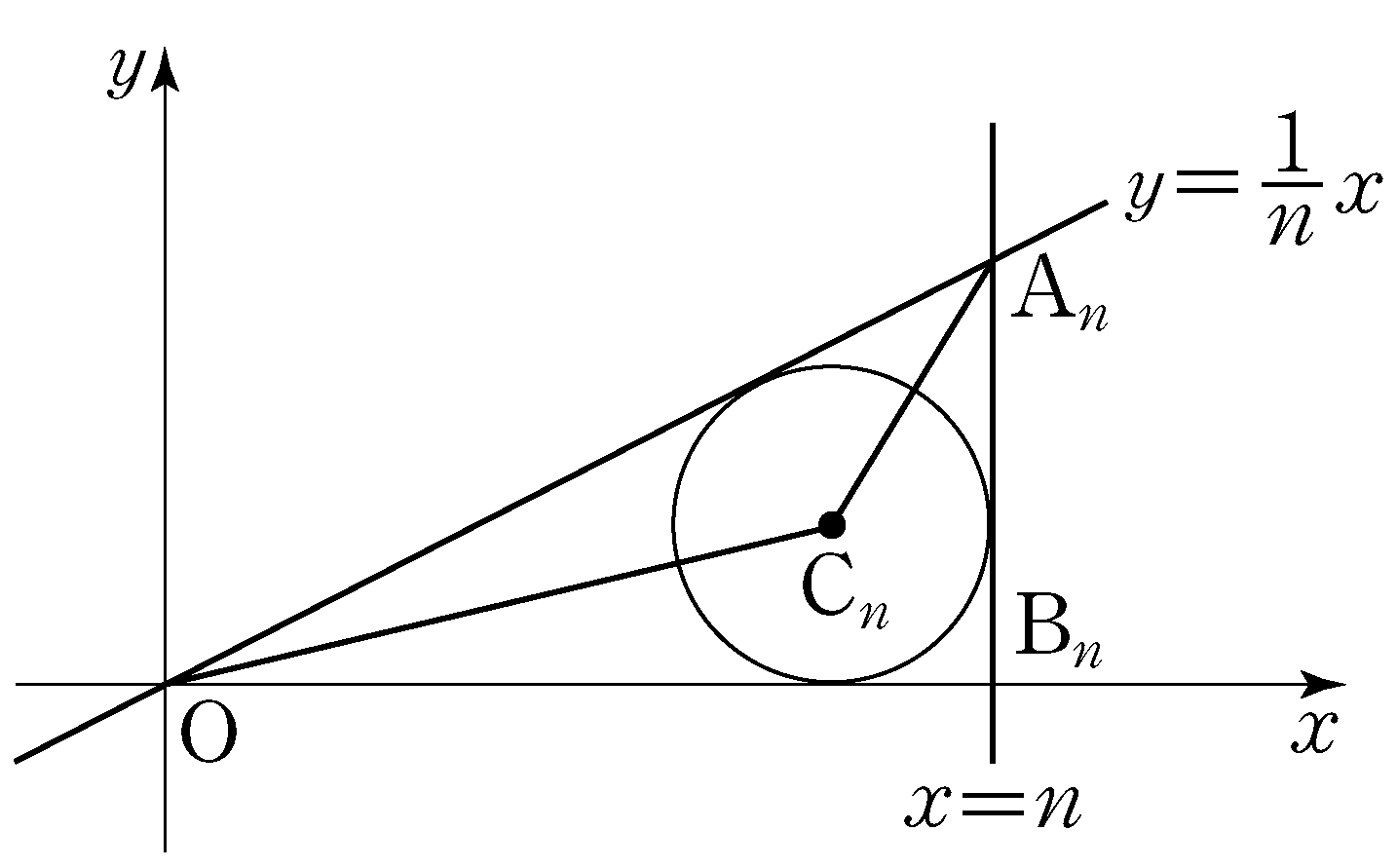
- \(5\)
- \(4\)
- \(3\)
- \(2\)
- \(1\)
Mathematics (Type Na)
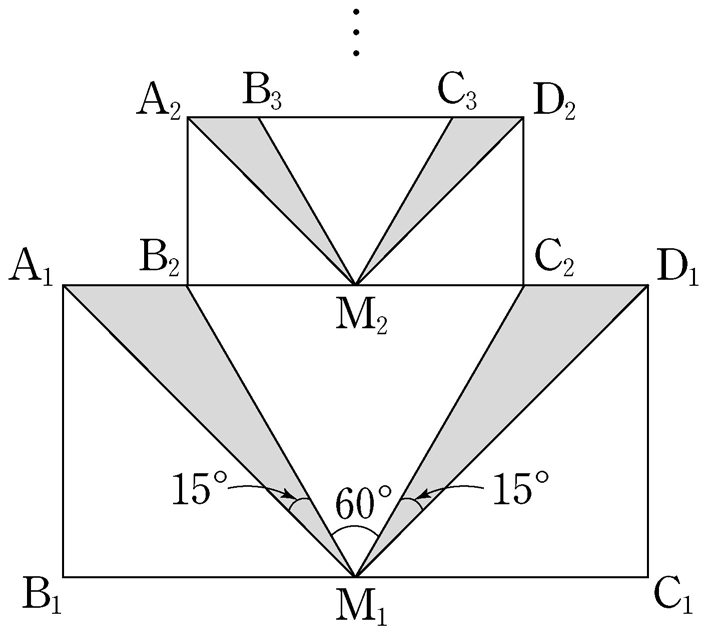
As the figure shows, Let \(\mathrm{A_2}\) and \(\mathrm{D_2}\) be points such that the quadrilateral \(\mathrm{A_2B_2C_2D_2}\) is a rectangle where \(\overline{\mathrm{B_2C_2}}=2\overline{\mathrm{A_2B_2}}\). Let \(\mathrm{M_2}\) be the midpoint of the line segment \(\mathrm{B_2C_2}\), and let \(\mathrm{B_3}\) and \(\mathrm{C_3}\) be two points on the line segment \(\mathrm{A_2D_2}\) such that \(\angle\mathrm{A_2M_2B_3}=\angle\mathrm{C_3M_2D_2}=15°\) and \(\angle\mathrm{B_3M_2C_3}=60°\). Let \(S_2\) be the sum of the area of triangles \(\mathrm{A_2M_2B_3}\) and \(\mathrm{C_3M_2D_2}\).
For all \(S_n\) obtained by repeating this process, what is the value of \(\displaystyle\sum_{n=1}^\infty S_n\)? [4 points]
- \(\dfrac{2+\sqrt{3}}{6}\)
- \(\dfrac{3-\sqrt{3}}{2}\)
- \(\dfrac{4+\sqrt{3}}{9}\)
- \(\dfrac{5-\sqrt{3}}{5}\)
- \(\dfrac{7-\sqrt{3}}{8}\)
\(y\)-axis, and then translating that graph \(3\) units horizontally and \(2\) units vertically. Given that this graph passes through the point \((1,4)\), what is the value of the positive number \(a\)?
- \(\sqrt{2}\)
- \(2\)
- \(2\sqrt{2}\)
- \(4\)
- \(4\sqrt{2}\)
\(S=\{(a \;\: b)|a+b\ne 0\}\),
\(T=\left\{\!\begin{pmatrix}
p \\ q
\end{pmatrix} \middle| \:pq\ne 0\right\}\)
For an element \(A\) in \(S\), Which option only contains every correct statement in the <List>?
[4 points]
- For all elements \(P\) in set \(T\), \(PA\) does not have an inverse matrix.
- For an element \(B\) in set \(S\) and an element \(P\) in set \(T\), if \(PA=PB\,\) then \(A=B\).
- There is an element \(P\) in set \(T\) that satisfies \(PA\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}\).
- a
- c
- a, b
- b, c
- a, b, c