2011 College Scholastic Ability Test

Mathematics (Type Ga)

What is the value of \(4^{\frac{3}{2}}\times\log_3\sqrt{3}\)? [2 points]
  1. \(5\)
  2. \(4\)
  3. \(3\)
  4. \(2\)
  5. \(1\)
For matrices \(A=\begin{pmatrix*}[r] 1 & -1 \\ 1 & 1 \end{pmatrix*}\) and \(B=\begin{pmatrix*}[r] 1 & 1 \\ -1 & 1 \end{pmatrix*}\), what is the sum of all of the elements in the matrix \(A(A+B)\)? [2 points]
  1. \(1\)
  2. \(2\)
  3. \(3\)
  4. \(4\)
  5. \(5\)
In \(3\)-dimensional space, the distance between points \(\mathrm{P}(0, 3, 0)\) and \(\mathrm{A}(-1, 1, a)\) is \(2\) times the distance between points \(\mathrm{P}\) and \(\mathrm{B}(1, 2, -1)\). What is the value of the positive number \(a\)? [2 points]
  1. \(\sqrt{7}\)
  2. \(\sqrt{6}\)
  3. \(\sqrt{5}\)
  4. \(2\)
  5. \(\sqrt{3}\)
Consider the following algebraic equation.
\(\sqrt{4x^2-5x+7}-4x^2+5x=1\)
What is the product of all real solutions of this equation? [3 points]
  1. \({-\dfrac{1}{2}}\)
  2. \({-\dfrac{3}{2}}\)
  3. \({-\dfrac{5}{2}}\)
  4. \({-\dfrac{7}{2}}\)
  5. \({-\dfrac{9}{2}}\)

Mathematics (Type Ga)

On the \(xy\)-plane, consider the point \(\mathrm{A}(0, 4)\) and a point \(\mathrm{P}\) on the ellipse \(\dfrac{x^2}{5}+y^2=1\). Among the two points where a line passing through points \(\mathrm{A}\) and \(\mathrm{P}\) meets the circle \(x^2+(y-3)^2=1\), let \(\mathrm{Q}\) be the point that is not point \(\mathrm{A}\). As point \(\mathrm{P}\) goes through every point on the ellipse, what is the length of the shape created by point \(\mathrm{Q}\)? [3 points]
  1. \(\dfrac{\pi}{6}\)
  2. \(\dfrac{\pi}{4}\)
  3. \(\dfrac{\pi}{3}\)
  4. \(\dfrac{2}{3}\pi\)
  5. \(\dfrac{3}{4}\pi\)
At some event hall, there are \(5\) places where one banner can be installed. There are three types of banners \(\mathrm{A}\), \(\mathrm{B}\) and \(\mathrm{C}\), and we have \(1\) banner of type \(\mathrm{A}\), \(4\) of type \(\mathrm{B}\), and \(2\) of type \(\mathrm{C}\). If we install \(5\) of our banners in the \(5\) places such that the following is satisfied, how many cases are possible as the result? (※ Banners of the same type are not considered distinct.) [3 points]
  1. Type \(\mathrm{A}\) should be installed.
  2. Type \(\mathrm{B}\) is installed in at least \(2\) places.
  1. \(55\)
  2. \(65\)
  3. \(75\)
  4. \(85\)
  5. \(95\)

Mathematics (Type Ga)

Cheolsu participates in a design contest. Participants receive scores in two categories, and \(3\) kinds of scores can be earned in each category as shown in the table. In each category, the probability that Cheolsu will receive score \(\mathrm{A}\), score \(\mathrm{B}\) and score \(\mathrm{C}\) are \(\dfrac{1}{2}\), \(\dfrac{1}{3}\) and \(\dfrac{1}{6}\) respectively. If the event of receiving the audience vote score and the event of receiving the judge panel score are independent, what is the probability that the \(2\) scores Cheolsu receive add up to \(70\)? [3 points]
Score
Category
 Score \(\mathrm{A}\) Score \(\mathrm{B}\) Score \(\mathrm{C}\)
Audience vote \(40\) \(30\) \(20\)
Judge panel \(50\) \(40\) \(30\)
  1. \(\dfrac{1}{3}\)
  2. \(\dfrac{11}{36}\)
  3. \(\dfrac{5}{18}\)
  4. \(\dfrac{1}{4}\)
  5. \(\dfrac{2}{9}\)
Consider the function
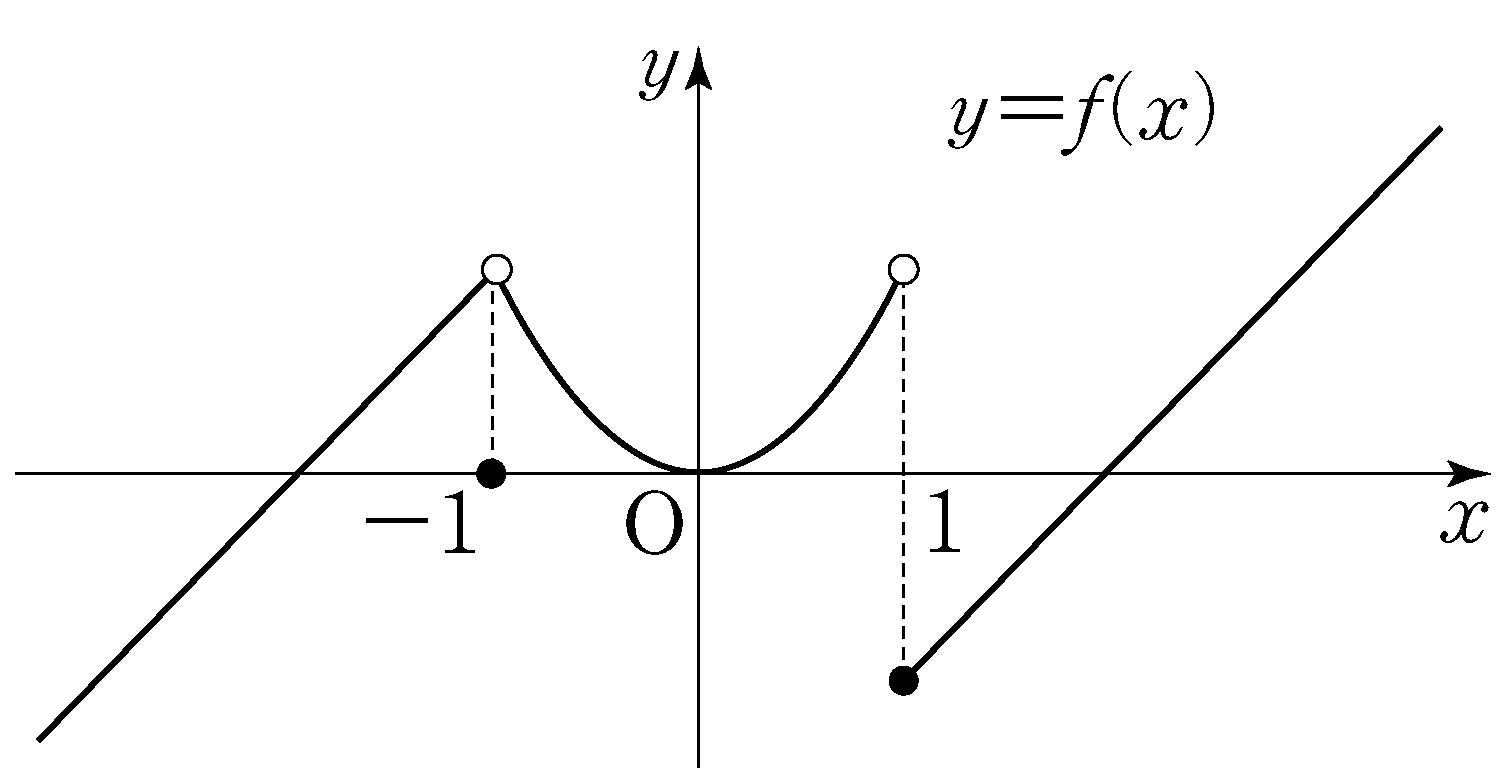
\(f(x)=\begin{cases} x+2 & \; (x<-1)\\ 0 & \; (x=-1)\\ x^2 & \; (-1<x<1)\\ x-2 & \; (x\geq 1). \end{cases}\)
Which option only contains every correct statement in the <List>? [3 points]
  1. \(\displaystyle\lim_{x\to 1+0}\{f(x)+f(-x)\}=0\)
  2. The function \(f(x)-|f(x)|\) has a discontinuity at exactly \(1\) point.
  3. There is no constant \(a\) for which the function \(f(x)f(x-a)\) is continuous on the set of all real numbers.
  1. a
  2. a, b
  3. a, c
  4. b, c
  5. a, b, c

Mathematics (Type Ga)

The relative density of the ground can be measured by inserting a probe into the ground. Let \(S\) be the effective vertical stress of the ground, and let \(R\) be the resistance to the probe while inserting to the ground. The relative density of the ground \(D(\%)\) can be calculated as follows.
\(D=-98+66\log\dfrac{R}{\sqrt{S}}\)
(※ The units of \(S\) and \(R\) are \(\text{metric ton/m}^2\).)
The effective vertical stress of ground \(\mathrm{A}\) is \(2\) times the effective vertical stress of ground \(\mathrm{B}\), and the resistance to the probe while inserting to ground \(\mathrm{A}\) is \(1.5\) times the resistance to the probe while inserting to ground \(\mathrm{B}\). If the relative density of ground \(\mathrm{B}\) is \(65(\%)\), what is the relative density of ground \(\mathrm{A}\)?
(※ Suppose \(\log2=0.3\).) [3 points]
  1. \(81.5\)
  2. \(78.2\)
  3. \(74.9\)
  4. \(71.6\)
  5. \(68.3\)
There is a rectangle \(\mathrm{A_1B_1C_1D_1}\) where \(\overline{\mathrm{A_1B_1}}=1\) and \(\overline{\mathrm{B_1C_1}}=2\). As the figure shows, let \(\mathrm{M_1}\) be the midpoint of the line segment \(\mathrm{B_1C_1}\), and let \(\mathrm{B_2}\) and \(\mathrm{C_2}\) be two points on the line segment \(\mathrm{A_1D_1}\) such that \(\angle\mathrm{A_1M_1B_2}=\angle\mathrm{C_2M_1D_1}=15°\) and \(\angle\mathrm{B_2M_1C_2}=60°\). Let \(S_1\) be the sum of the area of triangles \(\mathrm{A_1M_1B_2}\) and \(\mathrm{C_2M_1D_1}\).
As the figure shows, Let \(\mathrm{A_2}\) and \(\mathrm{D_2}\) be points such that the quadrilateral \(\mathrm{A_2B_2C_2D_2}\) is a rectangle where \(\overline{\mathrm{B_2C_2}}=2\overline{\mathrm{A_2B_2}}\). Let \(\mathrm{M_2}\) be the midpoint of the line segment \(\mathrm{B_2C_2}\), and let \(\mathrm{B_3}\) and \(\mathrm{C_3}\) be two points on the line segment \(\mathrm{A_2D_2}\) such that \(\angle\mathrm{A_2M_2B_3}=\angle\mathrm{C_3M_2D_2}=15°\) and \(\angle\mathrm{B_3M_2C_3}=60°\). Let \(S_2\) be the sum of the area of triangles \(\mathrm{A_2M_2B_3}\) and \(\mathrm{C_3M_2D_2}\).
For all \(S_n\) obtained by repeating this process, what is the value of \(\displaystyle\sum_{n=1}^\infty S_n\)? [4 points]
  1. \(\dfrac{2+\sqrt{3}}{6}\)
  2. \(\dfrac{3-\sqrt{3}}{2}\)
  3. \(\dfrac{4+\sqrt{3}}{9}\)
  4. \(\dfrac{5-\sqrt{3}}{5}\)
  5. \(\dfrac{7-\sqrt{3}}{8}\)

Mathematics (Type Ga)

As the figure shows, there is a plane \(\alpha\) and two disks with radius \(1\) whose centers are \(\sqrt{3}\) apart.
a line \(l\) passing through the centers of each disk is perpendicular to the face of each disk, and the angle between line \(l\) and plane \(\alpha\) is \(60°\). Suppose light rays are projected in a direction perpendicular to plane \(\alpha\) as shown in the figure. What is the area of the shadow on plane \(\alpha\) created by the two disks?
(※ Ignore the thickness of the disks.) [4 points]
  1. \(\dfrac{\sqrt{3}}{3}\pi+\dfrac{3}{8}\)
  2. \(\dfrac{2}{3}\pi+\dfrac{\sqrt{3}}{4}\)
  3. \(\dfrac{2\sqrt{3}}{3}\pi+\dfrac{1}{8}\)
  4. \(\dfrac{4}{3}\pi+\dfrac{\sqrt{3}}{16}\)
  5. \(\dfrac{2\sqrt{3}}{3}\pi+\dfrac{3}{4}\)
A set \(S\) whose elements are \(1\times2\) matrices and a set \(T\) whose elements are \(2\times1\) matrices are as follows.
\(S=\{(a \;\: b)|a+b\ne 0\}\), \(T=\left\{\!\begin{pmatrix} p \\ q \end{pmatrix} \middle| \:pq\ne 0\right\}\)
For an element \(A\) in \(S\), Which option only contains every correct statement in the <List>? [4 points]
  1. For all elements \(P\) in set \(T\), \(PA\) does not have an inverse matrix.
  2. For an element \(B\) in set \(S\) and an element \(P\) in set \(T\), if \(PA=PB\,\) then \(A=B\).
  3. There is an element \(P\) in set \(T\) that satisfies \(PA\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}\).
  1. a
  2. c
  3. a, b
  4. b, c
  5. a, b, c

Mathematics (Type Ga)

For customers of some traditional market, the distance from home to market follows a normal distribution with a mean of \(1740\text{m}\) and a standard deviation of \(500\text{m}\). \(15\%\) of customers whose distance from home to market is not less than \(2000\text{m}\), and \(5\%\) of customers whose distance from home to market is less than \(2000\text{m}\), drives their car to the market. If we randomly choose a customer who drove their car to the market, what is the probability that the distance from home to market of this customer is less than \(2000\text{m}\)?
(※ For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(0 \leq Z \leq 0.52) = 0.2\).) [4 points]
  1. \(\dfrac{3}{8}\)
  2. \(\dfrac{7}{16}\)
  3. \(\dfrac{1}{2}\)
  4. \(\dfrac{9}{16}\)
  5. \(\dfrac{5}{8}\)
As the figure shows, on the \(xy\)-plane, there are two points \(\mathrm{A}\) and \(\mathrm{B}\) on the \(x\)-axis. A parabola \(p_1\) whose vertex is \(\mathrm{A}\) and a parabola \(p_2\) whose vertex is \(\mathrm{B}\) satisfy the following. What is the area of the triangle \(\mathrm{ABC}\)? [4 points]
  1. The focus of \(p_1\) is \(\mathrm{B}\), and the focus of \(p_2\) is the origin \(\mathrm{O}\).
  2. \(p_1\) and \(p_2\) meet at two points \(\mathrm{C}\) and \(\mathrm{D}\) that are both on the \(y\)-axis.
  3. \(\overline{\mathrm{AB}}=2\)
  1. \(4(\sqrt{2}-1)\)
  2. \(3(\sqrt{3}-1)\)
  3. \(2(\sqrt{5}-1)\)
  4. \(\sqrt{3}+1\)
  5. \(\sqrt{5}+1\)

Mathematics (Type Ga)

A sequence \(\{a_n\}\) satisfies \(a_1=1\) and
\(a_{n+1}=n+1+\dfrac{(n-1)!}{a_1a_2\cdots a_n} \;(n\geq 1)\).
The following is a part of the process of computing the general term \(a_n\).
The following is true for all positive integers \(n\).
\(a_1a_2\cdots a_n a_{n+1}\)
\(= a_1a_2\cdots a_n\times(n+1)+(n-1)!\)
Let \(b_n=\dfrac{a_1a_2\cdots a_n}{n!}\). Then, \(b_1=1\) and
\(b_{n+1}=b_n + \fbox{\(\;(\alpha)\;\)}\).
The general term of the sequence \(\{b_n\}\) is
\(b_n=\fbox{\(\;(\beta)\;\)}\), therefore \(\dfrac{a_1a_2\cdots a_n}{n!}=\fbox{\(\;(\beta)\;\)}\).
\(\vdots\)
Therefore \(a_1=1\), and \(a_n=\dfrac{(n-1)(2n-1)}{2n-3} \: (n\geq 2)\).
Let \(f(n)\) be the correct expression for \((\alpha)\), and \(g(n)\) be the correct expression for \((\beta)\). What is the value of \(f(13)\times g(7)\)? [4 points]
  1. \(\dfrac{1}{70}\)
  2. \(\dfrac{1}{77}\)
  3. \(\dfrac{1}{84}\)
  4. \(\dfrac{1}{91}\)
  5. \(\dfrac{1}{98}\)
On the \(xy\)-plane, let \(\mathrm{P}(x_1,y_1)\) and \(\mathrm{Q(x_2,y_2)}\) be points where two curves \(y=|\log_2 x|\) and \(y=\!\left(\!\dfrac{1}{2}\!\right)^{\!\!x}\) meet \((x_1<x_2)\). Let \(\mathrm{R}(x_3,y_3)\) be the point where two curves \(y=|\log_2 x|\) and \(y=2^x\) meet. Which option only contains every correct statement in the <List>? [4 points]
  1. \(\dfrac{1}{2}<x<1\)
  2. \(x_2y_2-x_3y_3=0\)
  3. \(x_2(x_1-1)>y_1(y_2-1)\)
  1. a
  2. c
  3. a, b
  4. b, c
  5. a, b, c

Mathematics (Type Ga)

Suppose a point \(\mathrm{P}\) starts from the origin and moves on the number line, and its velocity \(v(t)\) at time \(t\,(0\leq t\leq5)\) is as follows.
\(v(t)=\begin{cases} 4t & \; (0\leq t<1)\\ -2t+6 & \; (1\leq t<3)\\ t-3 & \; (3\leq t\leq 5)\\ \end{cases}\)
For a real number \(x\,(0<x<3)\), let \(f(x)\) be the minimum value among
the distance from \(t=0\) to \(t=x\),
the distance from \(t=x\) to \(t=x+2\), and
the distance from \(t=x+2\) to \(t=5\)
that point \(\mathrm{P}\) travels. Which option only contains every correct statement in the <List>? [4 points]
  1. \(f(1)=2\)
  2. \(\displaystyle f(2)-f(1)=\int_1^2 v(t)dt\)
  3. \(f(x)\) is differentiable at \(x=1\).
  1. a
  2. b
  3. a, b
  4. a, c
  5. b, c
Short Answer Questions
The function \(f(x)=(x-1)^2(x-4)+a\) has a local minimum value of \(10\). Compute the constant \(a\). [3 points]
Compute the value of the positive integer \(k\) for which the number of integers \(x\) satisfying
\(1+\dfrac{k}{x-k}\leq\dfrac{1}{x-1}\)
is \(3\). [3 points]

Mathematics (Type Ga)

Consider a region enclosed by two curves \(y=\sqrt{x}\) and \(y=\sqrt{-x+10}\), and the \(x\)-axis. The solid formed by rotating this region about the \(x\)-axis has a volume of \(a\pi\). Compute \(a\). [3 points]
In \(3\)-dimensional space, let \(\mathrm{A}\) be the point where the line \(\dfrac{x}{2}=y=z+3\) meets the plane \(\alpha : x+2y+2z=6\). The intersection of plane \(\alpha\) and a sphere with center \((1,-1,5)\) passing through point \(\mathrm{A}\), is a shape with an area of \(k\pi\). Compute \(k\). [3 points]
As the figure shows, there is an equilateral triangle \(\mathrm{ABC}\) and a circle \(\mathrm{O}\) with the line segment \(\mathrm{AC}\) as a diameter. Let \(\mathrm{D}\) be a point on the line segment \(\mathrm{BC}\) such that \(\angle\mathrm{DAB}=\dfrac{\pi}{15}\). For a point \(\mathrm{X}\) moving on the circle \(\mathrm{O}\), let \(\mathrm{P}\) be the point \(\mathrm{X}\) that minimizes the inner product \(\overrightarrow{\mathrm{AD}}\cdot\overrightarrow{\mathrm{CX}}\).
Given that \(\angle\mathrm{ACP}=\dfrac{q}{p}\pi\), compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]
For integers \(n\geq2\), let \(S\) be the set of all products of two distinct elements in the set
\(\big\{3^{2k-1} \,\big|\, k\) is an integer, \(1\leq k\leq n\big\}\).
Let \(f(n)\) be the number of elements in \(S\). For example, \(f(4)=5\). Compute \(\displaystyle\sum_{n=2}^{11} f(n)\). [4 points]

Mathematics (Type Ga)

Consider a quartic function \(f(x)\) with a leading coefficient of \(1\), where \(f(0)=3\) and \(f'(3)<0\). For a real number \(t\), let \(S\) be the set
\(\big\{a \,\big|\: |f(x)-t|\) is not differentiable at \(x=a \big\}\)
and let \(g(t)\) be the number of elements in set \(S\). Given that \(g(t)\) has a discontinuity only at \(t=3\) and \(t=19\), compute \(f(-2)\). [4 points]
For a positive integer \(m\), consider cube-shaped blocks of the same size that are stacked \(1\) block high in column \(1\), \(2\) blocks high in column \(2\), \(3\) blocks high in column \(3\), \(\cdots\), \(m\) blocks high in column \(m\). Let us perform the following trial repeatedly until there are no columns with an even number of blocks.
For each column with an even number of blocks, remove \(\dfrac{1}{2}\) of the blocks in that column.
After all trials are done, let \(f(m)\) be the sum of the number of blocks from column \(1\) to column \(m\). For example, \(f(2)=2, f(3)=5,\) and \(f(4)=6\). Given that
\(\displaystyle\lim_{n\to\infty}\dfrac{f(2^{n+1})-f(2^n)}{f(2^{n+2})}=\dfrac{q}{p}\),
compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

Mathematics (Type Ga)

Calculus
If \(\tan\dfrac{\theta}{2}=\dfrac{\sqrt{2}}{2}\), what is the value of \(\sec\theta\)?
(※ \(0<\theta<\dfrac{\pi}{2}\)) [3 points]
  1. \(3\)
  2. \(\dfrac{10}{3}\)
  3. \(\dfrac{11}{3}\)
  4. \(4\)
  5. \(\dfrac{13}{3}\)
On the \(xy\)-plane, what is the slope of the tangent line to the curve \(y^3=\ln(5-x^2)+xy+4\) at point \((2,2)\)? [3 points]
  1. \(-\dfrac{3}{5}\)
  2. \(-\dfrac{1}{2}\)
  3. \(-\dfrac{2}{5}\)
  4. \(-\dfrac{3}{10}\)
  5. \(-\dfrac{1}{5}\)
A function \(f(x)\) is differentiable on the set of all real numbers. It is given that \(f(2x)=2f(x)f'(x)\) for all real numbers \(x\), and
\(f(a)\!=\!0,\, \displaystyle\int_{2a}^{4a}\!\dfrac{f(x)}{x}dx=k\:(a\!>\!0,\,0\!<\!k\!<\!1)\).
What is the value of \(\displaystyle\int_{a}^{2a}\!\dfrac{f(x)}{x}dx\) in terms of \(k\)? [3 points]
  1. \(\dfrac{k^2}{4}\)
  2. \(\dfrac{k^2}{2}\)
  3. \(k^2\)
  4. \(k\)
  5. \(2k\)

Mathematics (Type Ga)

For all functions \(f(x)\) differentiable on the set of all real numbers that satisfies the following, what is the minimum value of \(\displaystyle\int_0^2\!f(x)dx\)? [4 points]
  1. \(f(0)=1\) and \(f'(0)=1\).
  2. If \(0<a<b<2\), then \(f'(a)\leq f'(b)\).
  3. In the interval \((0, 1)\), \(f''(x)=e^x\).
  1. \(\dfrac{1}{2}e-1\)
  2. \(\dfrac{3}{2}e-1\)
  3. \(\dfrac{5}{2}e-1\)
  4. \(\dfrac{7}{2}e-2\)
  5. \(\dfrac{9}{2}e-2\)
Short Answer Quesetions
As the figure shows, for a point \(\mathrm{P}\) on the circle \(x^2+y^2=1\) on the \(xy\)-plane, let \(\theta\,(0<\theta<\dfrac{\pi}{4})\) be the angle between the line segment \(\mathrm{OP}\) and the positive direction of the \(x\)-axis. Let \(\mathrm{Q}\) be the point where a line, passing through point \(\mathrm{P}\) parallel to the \(x\)-axis, meets the curve \(y=e^x-1\). Let \(\mathrm{R}\) be the perpendicular foot from point \(\mathrm{Q}\) to the \(x\)-axis. Let \(\mathrm{T}\) be the intersection of line segments \(\mathrm{OP}\) and \(\mathrm{QR}\), and let \(S(\theta)\) be the area of the triangle \(\mathrm{ORT}\). Given that \(\displaystyle\lim_{\theta\to +0}\dfrac{S(\theta)}{\theta^3}=a\), compute \(60a\). [4 points]

Mathematics (Type Ga)

Probability & Statistics
The probability mass function of a discrete random variable \(X\) is given as
\(\mathrm{P}(X=x)=\dfrac{ax+2}{10}\;\;(x=-1,0,1,2)\).
What is the value of \(\mathrm{V}(3X+2)\), the variance of the random variable \(3X+2\)? (※ \(a\) is a constant.) [3 points]
  1. \(9\)
  2. \(18\)
  3. \(27\)
  4. \(36\)
  5. \(45\)
\(4\) male players and \(4\) female players participate in a table tennis match. If we randomly make \(4\) groups of \(2\) people, what is the probability that there are exactly \(2\) groups consisting of one male and one female? [3 points]
  1. \(\dfrac{3}{7}\)
  2. \(\dfrac{18}{35}\)
  3. \(\dfrac{3}{7}\)
  4. \(\dfrac{24}{35}\)
  5. \(\dfrac{27}{35}\)
The daily output of employees of some company depends on how long they have been employed. The daily output of an employee who was employed for \(n\) months \((1\leq n \leq 100)\) follows a normal distribution with a mean of \(an+100\) (\(a\) is a constant) and a standard deviation of \(12\). The probability that an employee who was employed for \(16\) months has a daily output of \(84\) or less is \(0.0228\).
What is the probability that an employee who was
employed for \(36\) months has a daily output between \(100\) and \(142\), computed using the standard normal table to the right? [3 points]
\(z\)\(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\)
\(1.0\)\(0.3413\)
\(1.5\)\(0.4332\)
\(2.0\)\(0.4772\)
\(2.5\)\(0.4938\)
  1. \(0.7745\)
  2. \(0.8185\)
  3. \(0.9104\)
  4. \(0.9270\)
  5. \(0.9710\)

Mathematics (Type Ga)

There are two data \(\mathrm{A}\) and \(\mathrm{B}\). Data \(\mathrm{A}\) consists of \(5\) distinct numbers, with the mean and the median both being \(25\). Data \(\mathrm{B}\) consists of \(7\) numbers, \(5\) of which are the same as data \(\mathrm{A}\), and the other two numbers being \(x\) and \(y\). Which option only contains every correct statement in the <List>? [4 points]
  1. If the mean of \(\mathrm{B}\) is \(25\), the median of \(\mathrm{B}\) is \(25\).
  2. If the mean of \(\mathrm{B}\) is \(27\) or more, at least one number between \(x\) and \(y\) is \(32\) or more.
  3. If \(x\) and \(y\) are both \(25\), the standard deviation of \(\mathrm{B}\) is less than the standard deviation of \(\mathrm{A}\).
  1. a
  2. c
  3. a, b
  4. b, c
  5. a, b, c
Short Answer Quesetions
Suppose we are researching the proportion of antibody holders among Korean adults for some disease. Let \(p\) be the proportion of antibody holders of the population, and let \(\hat{p}\) be the proportion of antibody holders of a sample of size \(n\) randomly sampled from the population. Compute the minimum value of \(n\) for which the probability that \(|\hat{p}-p|\leq0.16\sqrt{\hat{p}(1-\hat{p})}\) is at least \(0.9544\). (※ For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(0\leq|Z|\leq 2) = 0.4772\).) [4 points]

Mathematics (Type Ga)

Discrete Mathematics
Among the integer partitions of \(7\), what is the number of partitions where every part is \(3\) or less? [3 points]
  1. \(6\)
  2. \(7\)
  3. \(8\)
  4. \(9\)
  5. \(10\)
Let us add the least number of edges to the graph below to create a graph \(\mathrm{H}\) that has a Hamiltonian cycle. What is the number of distinct graphs \(\mathrm{H}\) that can be made? [3 points]
  1. \(30\)
  2. \(35\)
  3. \(40\)
  4. \(45\)
  5. \(50\)
A newly constructed building has \(6\) offices \(\mathrm{A,B,C,D,E}\) and \(\mathrm{F}\), and the price needed to build a computer network between two offices is shown in the table. What is the minimum price needed to build computer networks such that all \(6\) offices are connected via the network?
(Unit: million won)
\( \)\(\mathrm{A}\)\(\mathrm{B}\)\(\mathrm{C}\)\(\mathrm{D}\)\(\mathrm{E}\)\(\mathrm{F}\)
\(\mathrm{A}\)\( \)\(5\)\(4\)\(2\)\(2\)\(1\)
\(\mathrm{B}\)\(5\)\( \)\(5\)\(3\)\(5\)\(5\)
\(\mathrm{C}\)\(4\)\(5\)\( \)\(4\)\(5\)\(6\)
\(\mathrm{D}\)\(2\)\(3\)\(4\)\( \)\(3\)\(3\)
\(\mathrm{E}\)\(2\)\(5\)\(5\)\(3\)\( \)\(3\)
\(\mathrm{F}\)\(1\)\(5\)\(6\)\(3\)\(3\)\( \)
  1. \(11\) million won
  2. \(12\) million won
  3. \(13\) million won
  4. \(14\) million won
  5. \(15\) million won

Mathematics (Type Ga)

For the following graph \(\mathrm{G}\) with \(7\) vertices, which option only contains every correct statement in the <List>? [4 points]
  1. The minimum spanning tree of graph \(\mathrm{G}\) has
    \(6\) edges.
  2. Graph \(\mathrm{G}\) is not a planar graph.
  3. The smallest number of colors needed for a proper vertex coloring of graph \(\mathrm{G}\) is \(3\).
  1. a
  2. b
  3. c
  4. a, b
  5. a, c
Short Answer Quesetions
Among the strings of length \(n\) consisting of characters \(a, b\) and \(c\) where each character can be used multiple times, let \(a_n\) be the number of strings that satisfy the following.
  1. The first and last characters are both \(a\).
  2. Only \(a\) can come right after \(b\) or \(c\).
The sequence \(\{a_n\}\) satisfies \(a_1=1, a_2=1\), and the recurrence relation
\(a_{n+2}=a_{n+1}+pa_n\;\;(n\geq1)\).
Given that \(a_7=q\), compute \(p+q\). [4 points]