1997 College Scholastic Ability Test

Mathematics·Studies (I)

Nat. Sciences

What is the value of \((125^2-75^2)\div\{5+(30-50)\div(-4)\}\)? [2 points]

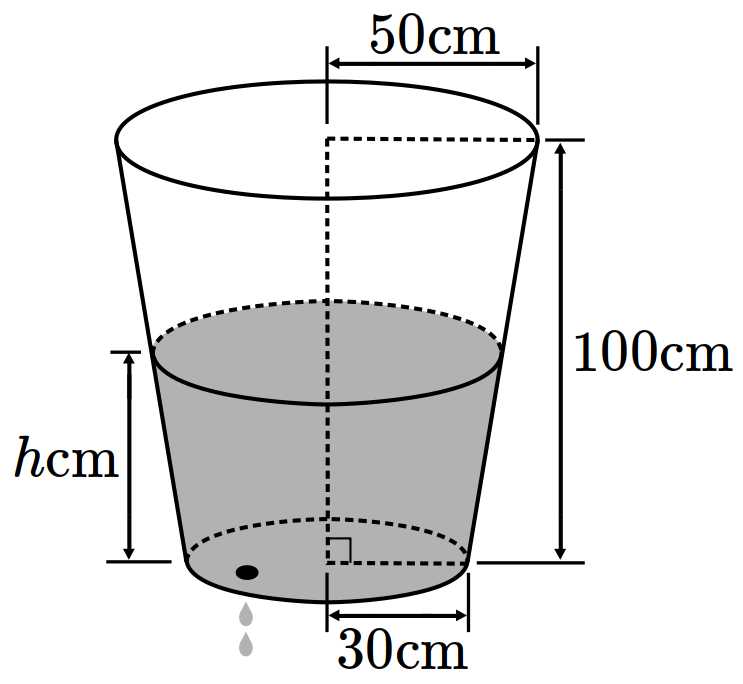
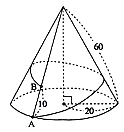
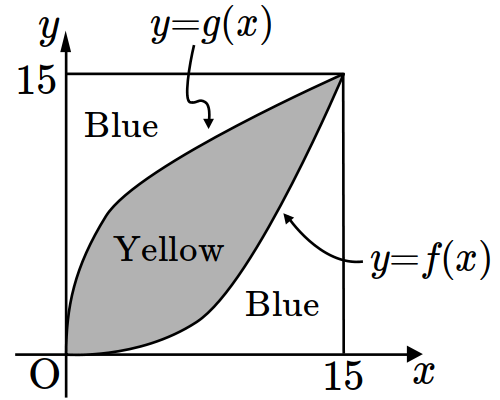
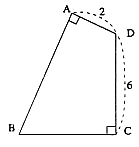
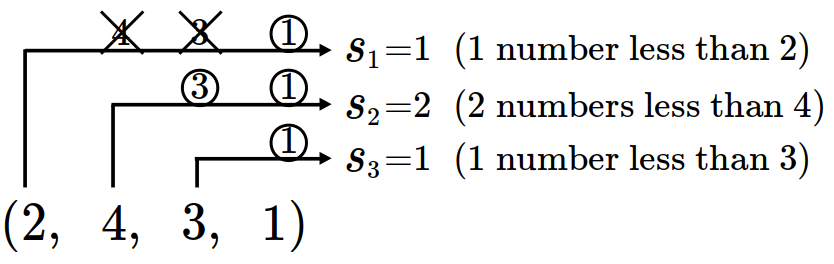\(75\)
\(125\)
\(900\)
\(1000\)
\(1225\)

For \(\alpha=-2+i\) and \(\beta=1-2i\), what is the value of \(\alpha\overline{\alpha}+\overline{\alpha}\beta+\alpha\overline{\beta}+\beta\overline{\beta}\)? (※ \(\overline{\alpha}\) and \(\overline{\beta}\) are complex conjugates of \(\alpha\) and \(\beta\) respectively, and \(i=\sqrt{-1}\).) [2 points]

\(1\)
\(2\)
\(4\)
\(10\)
\(20\)

The angle between two vectors \(\vec{a}\) and \(\vec{b}\) is \(60°\). The magnitude of \(\vec{b}\) is \(1\), and The magnitude of \(\vec{a}-3\vec{b}\) is \(\sqrt{13}\). What is the magnitude of \(\vec{a}\)? [2 points]

\(1\)
\(3\)
\(4\)
\(5\)
\(7\)

What is the value of \(\displaystyle\lim_{x\to0}\frac{\sin(3x^3+5x^2+4x)}{2x^3+2x^2+x}\)? [3 points]

\(4\)
\(3\)
\(\dfrac{3}{2}\)
\(1\)
\(\dfrac{\sin3}{2}\)

Mathematics·Studies (I)

Nat. Sciences

For the universe \(U\) and its two subsets \(A\) and \(B\), let us define

\(A*B=(A\cap B)\cup(A\cup B)^C\).

Which option below is not always true? (※ \(U\ne\varnothing\)) [2 points]

\(A*U=U\)
\(A*B=B*A\)
\(A*\varnothing=A^C\)
\(A*B=A^C*B^C\)
\(A*A^C=\varnothing\)

Consider a linear map that maps the point \(\mathrm{P}(2,0)\) to point \(\mathrm{Q}\left(\!\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\!\right)\), and the point \(\mathrm{R}(0,2)\) to point \(\mathrm{S}\left(\!-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\!\right)\). Let \(A\) be the matrix that represents this linear map. Given that \(A^4\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}\), what is the value of \(\dfrac{a+bi}{1+i}\)? (※ \(i=\sqrt{-1}\)) [2 points]

\(-\dfrac{1}{16}\)
\(\dfrac{\sqrt{2}}{8}\)
\(\dfrac{1}{16}i\)
\(\dfrac{\sqrt{2}+i}{8}\)
\(\dfrac{-1+\sqrt{2}}{16}\)

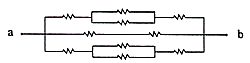
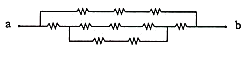
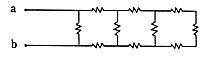
Figure below is a circuit using \(10\) identical resistors (

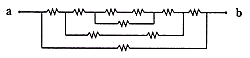
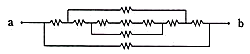
). Which option below has the same topology with this circuit? [2 points]

The annual soft drink sales of some soft drink company greatly depends on the average temperature in summer that year. According to past data, the probability that the annual sales quota is reached is \(0.8\) if the average temperature in summer that year is higher than the previous year, \(0.6\) if it is about the same as the previous year, and \(0.3\) if it is lower than the previous year.
According to the weather forecast, the average temperature in summer next year will be higher than this year for a probability of \(0.4\), about the same as this year for a probability of \(0.5\), and lower than this year for a probability of \(0.1\). What is the probability that this company will reach quota in the next year? [2 points]

\(0.55\)
\(0.60\)
\(0.65\)
\(0.70\)
\(0.75\)

Mathematics·Studies (I)

Nat. Sciences

Consider a point \(\mathrm{A}(-1,0)\) on the parabola \(y=x(x+1)\). A point \(\mathrm{P}\) moves along the parabola, starting from point \(\mathrm{A}\), and approaches the origin \(\mathrm{O}\) arbitrarily closely. what is the limit of the size of \(\angle\mathrm{APO}\)? [3 points]

\(90°\)
\(120°\)
\(135°\)
\(150°\)
\(180°\)

A polynomial function \(P(x)\) satisfies the following identity.

\(P(P(x)+x)=(P(x)+x)^2-(P(x)+x)+1\)

What is the value of \(P'(0)\)? [3 points]

\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)

A function \(f(x)\) differentiable at all real numbers \(x\) satisfies the following.

\(f(1-x)=1-f(x)\)

Which option below is not always true? [3 points]

\(f(0)+f(1)=1\)
\(f'(0)=f'(1)\)
\(\displaystyle\int_0^1\!f(x)dx=\frac{1}{2}\)
\(f\!\left(\!\dfrac{1}{2}\!\right)=\dfrac{1}{2}\)
\(f(0)=0\)

For an absolutely continuous random variable \(X\) that follows a normal distribution with a mean of \(m\) and a standard deviation of \(\sigma\), it is known that the probability density function of \(X\) is

\(f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\,\large e^{-\small \dfrac{1}{2\sigma^2}(x\,-\,m\,)^2}\)
\((-\infty<x<\infty)\).

What is approximately the value of

\(\displaystyle\int_4^{6.6}\sqrt{\frac{2}{\pi}}\,\large e^{-\small \dfrac{(x-5)^2}{8}} \normalsize dx\)

computed using the following standard normal table? [2 points]

\(0.1199\)
\(0.3864\)
\(0.6826\)
\(0.9505\)
\(1.9184\)

\(z\)	\(\mathrm{P}(0<Z\leq z)\)
\(\begin{align}0.1\\0.2\\0.3\\0.4\\0.5\\0.6\\0.7\\0.8\\0.9\\1.0\end{align}\)	\(\begin{align}0.0398\\0.0793\\0.1179\\0.1554\\0.1915\\ 0.2257\\0.2580\\0.2881\\0.3159\\0.3413\end{align}\)

Mathematics·Studies (I)

Nat. Sciences

As the figure shows, \(\mathrm{A}\) and \(\mathrm{B}\) move in the same direction along a line. \(\mathrm{B}\) starts moving at the same time with \(\mathrm{A}\), \(200\) meters ahead of \(\mathrm{A}\).
Let \(a_1\) be the starting position of \(\mathrm{A}\), \(a_2\) be the starting position of \(\mathrm{B}\), \(a_3\) be the position of \(\mathrm{B}\) when \(\mathrm{A}\) reaches \(a_2\), and \(a_4\) be the position of \(\mathrm{B}\) when \(\mathrm{A}\) reaches \(a_3\). Continue this process for all points \(a_n(n=1,2,3,\cdots)\). If the velocity of \(\mathrm{A}\) is \(2\) times the velocity of \(\mathrm{B}\), what is the position of \(\mathrm{A}\) when the distance between \(\mathrm{A}\) and \(\mathrm{B}\) becomes less than \(1\) meter? [3 points]

Between \(a_4\) and \(a_5\)
Between \(a_6\) and \(a_7\)
Between \(a_8\) and \(a_9\)
Between \(a_{10}\) and \(a_{11}\)
Between \(a_{12}\) and \(a_{13}\)

A function \(f(x)\) defined for all real numbers is a periodic function satisfying \(f(x)=x^2\,(-1\leq x\leq1)\:\) and \(\:f(x+2)=f(x)\). On the \(xy\)-plane, for all positive integers \(n\), let \(a_n\) be the number of intersections between the line \(y=\dfrac{1}{2n}x+\dfrac{1}{4n}\) and the graph of the function \(y=f(x)\). What is the value of \(\displaystyle\lim_{n\to\infty}\!\frac{a_n}{n}\)? [2 points]

\(0\)
\(1\)
\(2\)
\(3\)
\(4\)

The two tangent lines to the parabola \(y=(x-a)^2+b\) at points \(\mathrm{P}(s+a,s^2+b)\) and \(\mathrm{Q}(t+a,t^2+b)\) respectively, are perpendicular to each other. Let \(A\) be the area of the shape enclosed by these two tangent lines and the parabola. Which option contains every correct statement in the <List>? [2 points]

If \(s\) increases, \(t\) also increases.
If \(a\) increases, the area \(A\) also increases.
If \(b\) changes, the area \(A\) also changes.

a
b
c
a, c
b, c

Members of the ‘base-\(12\) society’ write integers by using the mapping shown in the table below.

Base-\(10\)	\(1\;\:2\;\:3\;\:4\;\:5\;\:6\;\:7\;\:8\;\:9\;\:10\;\:11\;\:12\;\:13\;\:\cdots\)
Base-\(12\)	\(1\;\:2\;\:3\;\:4\;\:5\;\:6\;\:7\;\:8\;\:9\;\;\:x\;\;\:y\;\:\:\,10\;\:11\;\:\cdots\)

Some examples of addition in base-\(12\) are

\(1+9=x\:\) and \(\:x+y=19\).

For two base-\(12\) numbers \(xxx\) and \(yyy\), what is their sum \(xxx+yyy\) written in base-\(12\)? [3 points]

\(1779\)
\(2331\)
\(1xx9\)
\(1yy9\)
\(1yyx\)

Mathematics·Studies (I)

Nat. Sciences

The flowchart to the right is an algorithm finding the smallest positive integer \(n\) for which the inequality \(2^{n+1}<9n^4\) is false. What are appropriate for \((\alpha), (\beta)\) and \((\gamma)\) in the flowchart to the right in this order? [2 points]

\(S\!\gets\!S\!+\!2,\;S\geq 9N^4,\:\) Print \(N+1\)
\(S\!\gets\!S\!\times\!2,\;S< 9N^4,\:\) Print \(N\)
\(S\!\gets\!S\!\times\!2,\;S< 9N^4,\:\) Print \(N+1\)
\(S\!\gets\!S\!\times\!2,\;S\geq 9N^4,\:\) Print \(N\)
\(S\!\gets\!S\!\times\!2,\;S\geq 9N^4,\:\) Print \(N+1\)

The following is the middle part of a proof of the statement 「If \(x^2+y^2+z^2=1111\), then \(\fbox{\(\;(\alpha)\;\)}\)」.

<Proof>
\(\cdots\) (omitted) \(\cdots\)
In the division of integers \(x, y\) and \(z\) by \(8\),
the remainder is among \(0,1,2,3,4,5,6\) or \(7\). Therefore, in the division of \(x^2, y^2\) and \(z^2\) by \(8\), the remainder is among \(0,1\) or \(4\). Therefore, in the division of \(x^2+y^2+z^2\) by \(8\), the remainder is among \(0,1,2,3,4,5\) or \(6\). However, the division of \(1111\) by \(8\) has remainder \(7\).
\(\cdots\) (omitted) \(\cdots\)

What is appropriate for \(\fbox{\(\;(\alpha)\;\)}\) above? [2 points]

at least one among \(x, y\) and \(z\) is an integer.
none among \(x, y\) and \(z\) are integers.
there is at least one solution where \(x, y\) and \(z\) are all integers.
there is only one solution where \(x, y\) and \(z\) are all integers.
there are no solutions where \(x, y\) and \(z\) are all integers.

As the figure shows, a quadrilateral \(\mathrm{ABCD}\) is inscribed in a circle, and its two diagonals \(\mathrm{AC}\) and \(\mathrm{BD}\) meet at point \(\mathrm{P}\) perpendicular to each other. Let \(\mathrm{E}\) be the perpendicular foot from point \(\mathrm{P}\) to edge \(\mathrm{BC}\), and let \(\mathrm{F}\) be the point where line \(\mathrm{PE}\) meets the edge \(\mathrm{AD}\). Which option below cannot be proven from this? [3 points]

\(\angle\mathrm{CBP}=\angle\mathrm{PAD}\)
\(\angle\mathrm{APF}=\angle\mathrm{PAF}\)
\(\angle\mathrm{FPD}=\angle\mathrm{FDP}\)
\(\overline{\mathrm{AF}}=\overline{\mathrm{FD}}\)
\(\overline{\mathrm{AP}}=\overline{\mathrm{AF}}\)

What is the minimum distance from a point on the sphere \((x-1)^2+(y-2)^2+(z-3)^2=1\) to the plane \(x+y+z=10\)? [3 points]

\(\dfrac{3\sqrt{3}-3}{3}\)
\(\dfrac{4\sqrt{3}-3}{3}\)
\(\dfrac{3\sqrt{3}+2}{3}\)
\(\dfrac{2\sqrt{3}+5}{3}\)
\(\dfrac{3\sqrt{3}+5}{3}\)

Mathematics·Studies (I)

Nat. Sciences

It is the summer of the year \(2525\), and you are making plans for January \(2526\). You have the calendar of the current year (\(2525\)) from January to December, but you don't have the calendar for the New Year (January \(2526\)). What month in the \(2525\) calendar has the same number of dates, on the same day of the week, as the January \(2526\) calendar? [3 points]

March
May
July
August
No such month.

The electrons of some atom can be in three states \(a,b\) or \(c\) according to the variations in energy. Suppose the following rules hold.

Rule \(1\): If the energy increases, electrons in state \(b\) rise to state \(c\), and electrons in state \(a\) either rise to state \(b\) or to state \(c\).

Rule \(2\): If the energy decreases, electrons in state \(b\) fall to state \(a\), and electrons in state \(c\) either fall to state \(b\) or to state \(a\).

In <Phase \(1\)>, an electron is in state \(a\). If the energy increases to <Phase \(2\)>, this electron will be in state \(b\) or state \(c\). There are \(2\) possible paths for this electron, namely \(a\to b\) and \(a\to c\). If the energy decreases again to <Phase \(3\)>, the possible paths for this electron until this point is \(3\), namely \(a\to b\to a\), \(a\to c\to b\), and \(a\to c\to a\).
If the energy keeps alternately increasing and decreasing in this fashion, what is the number of possible paths for this electron from <Phase \(1\)> to <Phase \(7\)>? [3 points]

\(18\)
\(19\)
\(20\)
\(21\)
\(22\)

As the figure shows, there is a water tank completely filled with water, in the shape of a circular cone frustum with a height of \(100\,\text{cm}\), a top radius of \(50\,\text{cm}\), and a base radius of \(30\,\text{cm}\). A hole was made in the base of this water tank and water starts to leak. When the height from the base to the surface of the water is \(h\,\text{cm}\), the amount of water leaking out is \(4\sqrt{h}\,\text{cm}^3\) per second. What is the instantaneous rate of change of the height when \(h=50\)? (Unit: \(\text{cm}/\text{seconds}\)) [4 points]

\(-\dfrac{20\sqrt{2}}{\pi}\times10^{-2}\)
\(-\dfrac{5\sqrt{2}}{\pi}\times10^{-2}\)
\(-\dfrac{20\sqrt{2}}{9\pi}\times10^{-2}\)
\(-\dfrac{5\sqrt{2}}{4\pi}\times10^{-2}\)
\(-\dfrac{4\sqrt{2}}{5\pi}\times10^{-2}\)

† The original image to this question was lost.

There is a mountain in the shape of a right circular cone as the figure shows. A track of a sightseeing train is laid along the shortest possible path from point \(\mathrm{A}\) to point \(\mathrm{B}\) that wraps around the mountain once. This track is uphill at first but then becomes downhill. What is the length of the part of the track that is downhill? [4 points]

\(\dfrac{200}{\sqrt{19}}\)
\(\dfrac{300}{\sqrt{30}}\)
\(\dfrac{300}{\sqrt{91}}\)
\(\dfrac{400}{\sqrt{91}}\)
\(\dfrac{500}{\sqrt{91}}\)

† Options \(5\) was identical to option \(3\) in the source due to a typo.

Mathematics·Studies (I)

Nat. Sciences

Short Answers (25~30)

As the figure shows, a square tile is laid on the \(xy\)-plane with its horizontal and vertical sides aligning with the \(x\)-axis and \(y\)-axis, respectively. Suppose we color inside this tile with blue and yellow, with the graphs of \(y=f(x)\) and \(y=g(x)\) being the boundaries of the colors. Given that the areas of the region colored blue and the region colored yellow have a ratio of \(2:3\), compute \(\displaystyle\int_0^{15}f(x)dx\).
(※ \(g(x)\) is the inverse of the function \(f(x)\).) [2 points]

Let \(g(x)\) be the inverse of the function

\(f(x)=\begin{cases} \dfrac{71}{5}-\dfrac{19}{15}x & (x<12)\\\\ 1-2\log_3(x-9) & (x\geq12). \end{cases}\)

Compute the value of \(x\) that satisfies \((g\circ g\circ g\circ g\circ g)(x)=-3\).
(※ \((g\circ g)(x)=g\{g(x)\}\)) [3 points]

In the figure to the right, all sides of \(\square \mathrm{ABCD}\) are integers, and

\(\overline{\mathrm{AD}}=2,\;\overline{\mathrm{CD}}=6,\)
and \(\angle\mathrm{A}=\angle\mathrm{C}=90°\).

Compute the maximum perimeter of this quadrilateral. [3 points]

Let \((a_1,a_2,a_3,a_4)\) be a permutation of the set \(A=\{1,2,3,4\}\). Let \(s_k\,(k=1,2,3)\) be the number of elements to the right of \(a_k\) in the permutation that are less than \(a_k\).
Let us denote the sum \(s_1+s_2+s_3\) as

\(|\,(a_1,a_2,a_3,a_4)\,|\).

For example,

\(\begin{align}|\,(2,4,3,1)\,|\: &=\:s_1+s_2+s_3\\ &=\:1+2+1\:=\:4.\end{align}\)

For all \(24\) permutations \((i_1,i_2,i_3,i_4)\) of the set \(A\), determine the value of \(|\,(i_1,i_2,i_3,i_4)\,|\) and compute the sum of all such values. [4 points]

Mathematics·Studies (I)

Nat. Sciences

Two polynomial equations \(P(x)=0\) and \(Q(x)=0\) have \(7\) and \(9\) distinct real solutions, respectively,
and the set

\(A=\{(x,y)\,|\,P(x)Q(y)=0\:\) and \(\:Q(x)P(y)=0,\)
\(\qquad\;\; x\) and \(y\) are real numbers\(\}\)

is an infinite set. Let \(B\) be a subset of \(A\) where

\(B=\{(x,y)\,|\,(x,y)\in A\:\) and \(\:x=y\}\),

and let \(n(B)\) be the number of elements in \(B\). Then, the value of \(n(B)\) varies according to \(P(x)\) and \(Q(x)\). Compute the maximum value of \(n(B)\). [4 points]

Using approximations \(\log_{10}2=0.301\) and \(\log_{10}11=1.041\), compute the value of \(\log_{10}275\), and round the result to the nearest hundredth. [2 points]