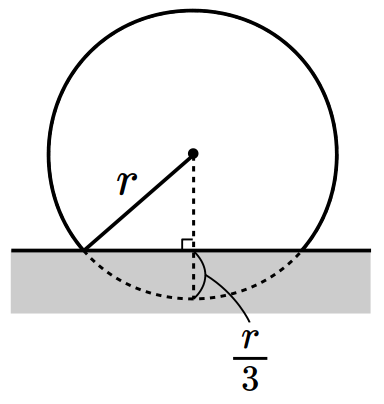
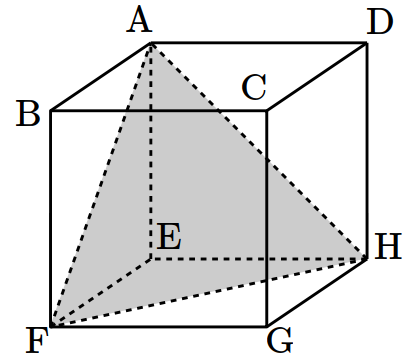
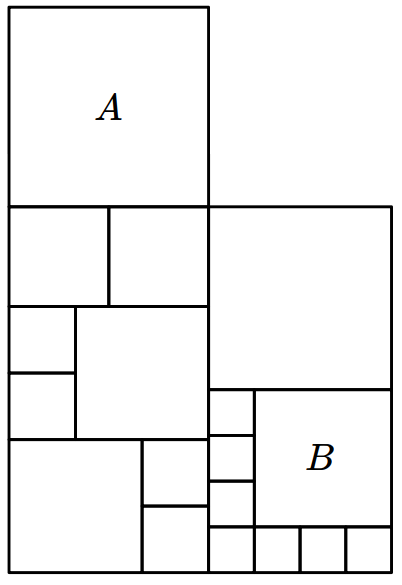
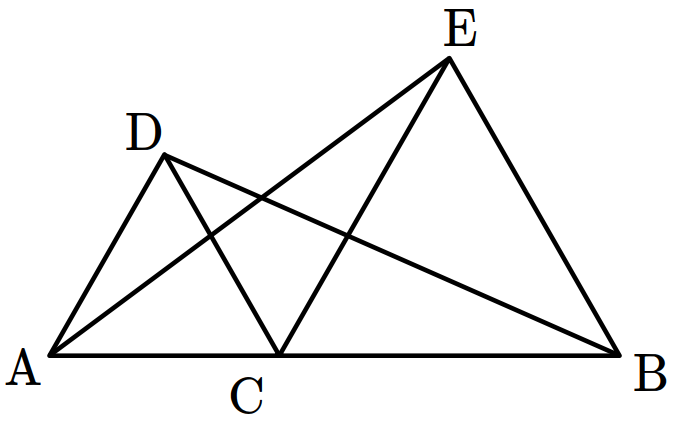
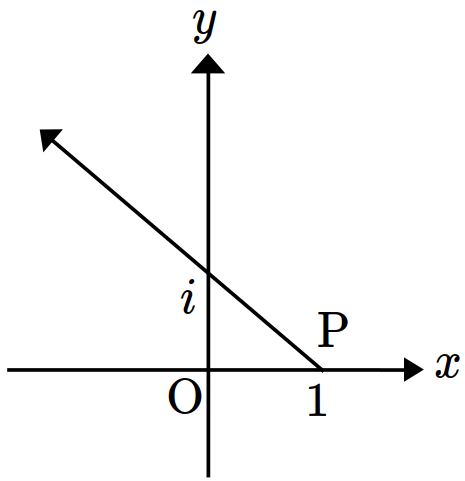
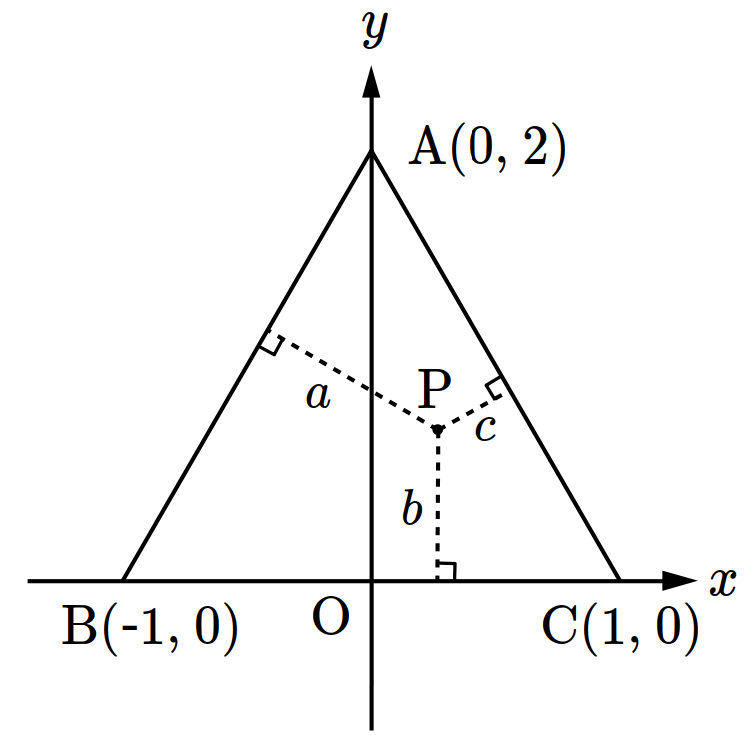
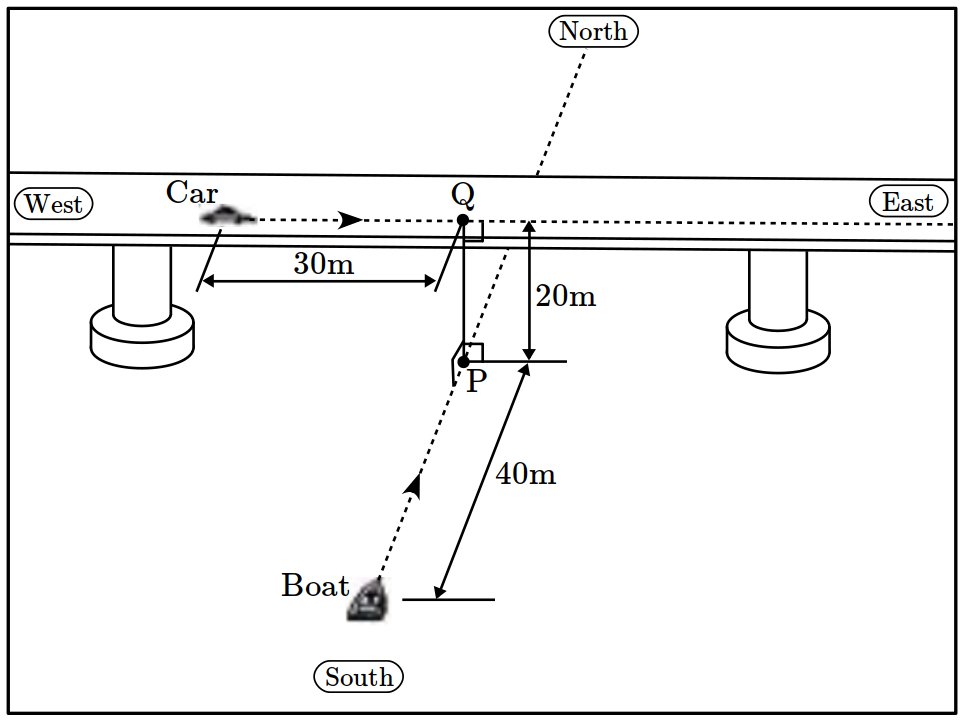
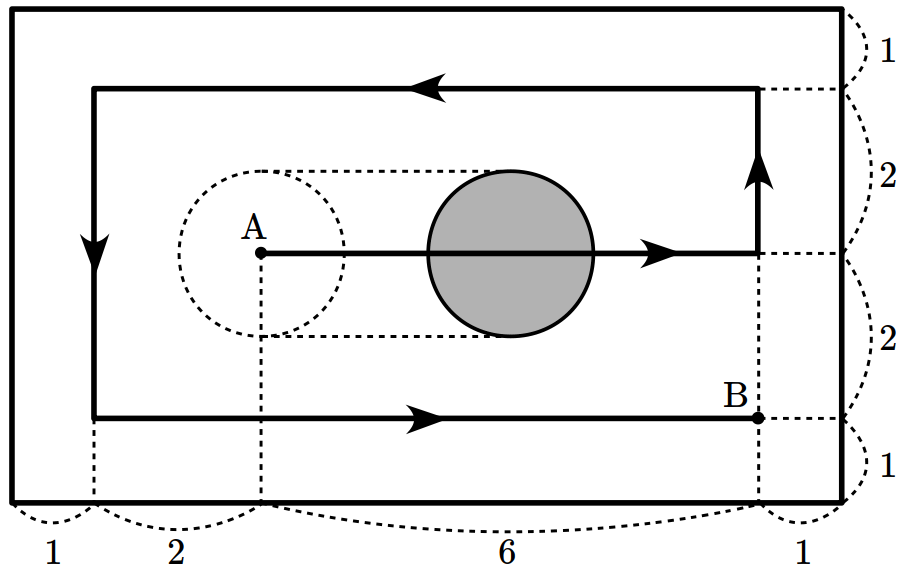
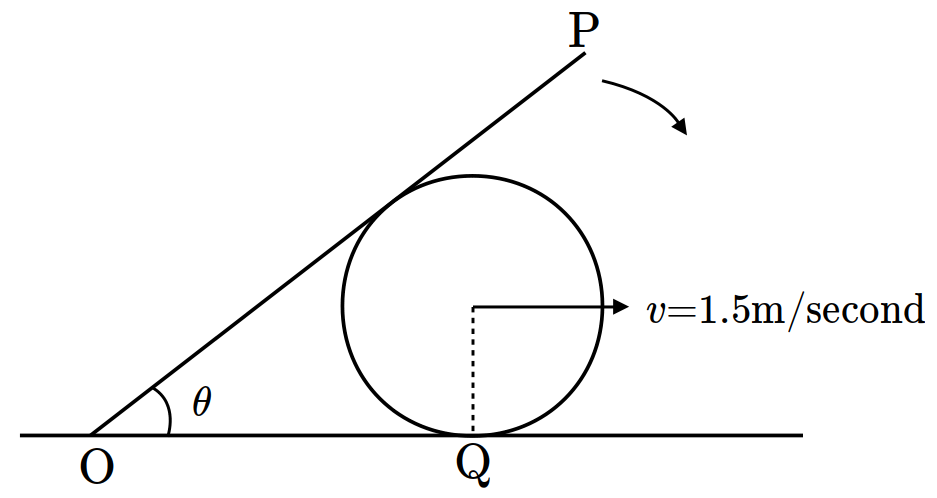
- \(8\)
- \(10\)
- \(12\)
- \(14\)
- \(16\)
Mathematics·Studies (I)
Nat. Sciences
- \(3\)
- \(4\)
- \(5\)
- \(6\)
- \(7\)
‘If \(\overline{\mathrm{AB}}=\overline{\mathrm{AC}}\), then \(\angle \mathrm{B} = \angle \mathrm{C}\).’ Which option contains all correct statements among the converse, inverse and contrapositive of this statement? [1 point]
- Contrapositive
- Converse and inverse
- Inverse and contrapositive
- Converse and contrapositive
- Converse, inverse and contrapositive
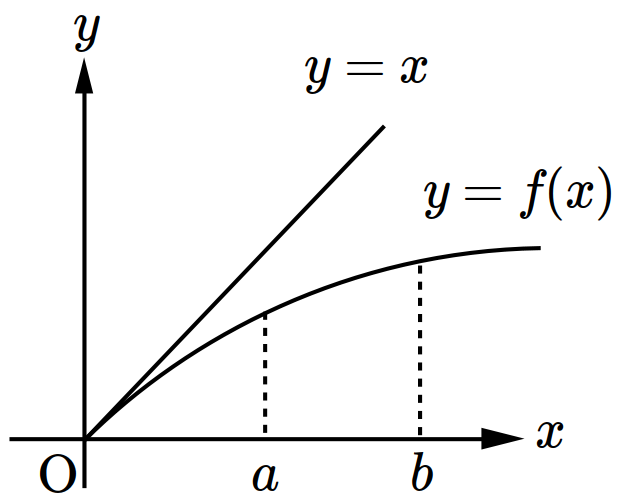
- \(\dfrac{f(a)}{a}< \dfrac{f(b)}{b}\)
- \(f(b)-f(a) > b-a\)
- \(f'(a) > f'(b)\)
- a
- b
- c
- a, b
- b, c
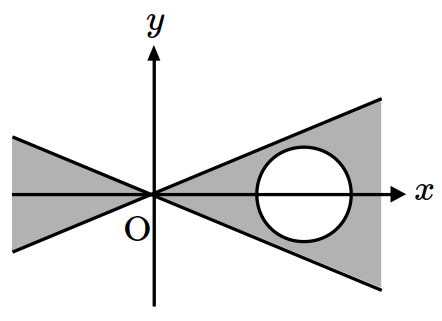
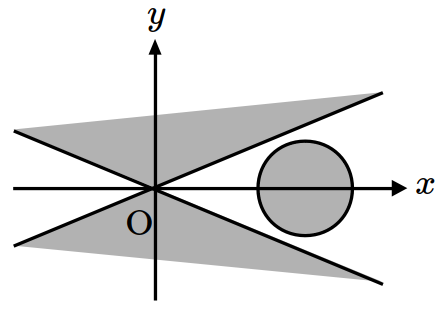
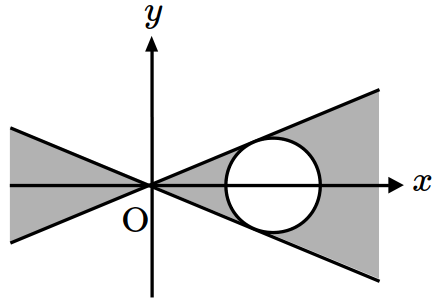
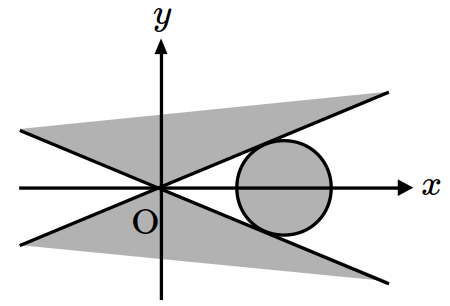
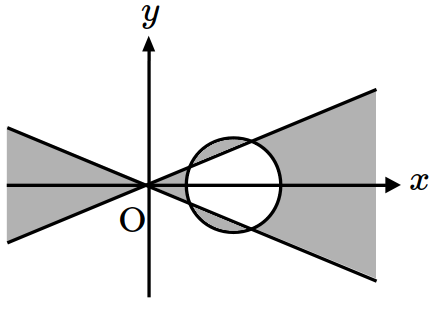
\(xy\)-plane satisfying \((x^2-4y^2)(x^2-6x+y^2+8)\leq 0\)? (※ The boundary of the colored region is included.) [1 point]